题目内容
【题目】如图，PA=PB，∠PAM+∠PBN=180°，求证：OP平分∠AOB．
【答案】详见解析
【解析】
过点P分别作PE⊥OM，PF⊥ON，垂足分别为E，F，根据等角的补角相等可得出∠PAE=∠PBF，结合∠AEP＝∠BFP、PA＝PB即可证出△APE≌△BPF（AAS），根据全等三角形的性质可得出PE＝PF，进而可证出OP平分∠AOB．
如图，过点P分别作PE⊥OM，PF⊥ON，垂足分别为E，F，
则∠PEA=∠PFB=90°．
又∵∠PAM+∠PBN=180°，∠PBF+∠PBN=180°，
∴∠PAM=∠PBF，即∠PAE=∠PBF．
在△PAE与△PBF中，
，
∴△PAE≌△PBF（AAS）．
∴PE=PF．
又∵PE⊥OM，PF⊥ON，
∴OP平分∠AOB．
练习册系列答案
相关题目
【题目】某校组织七年级学生体育健康抽测，（1）班25名学生的成绩（满分为100分）统计如下：
90，74，88，65，98，76，81，42，85，70，55，80，95，88，72，87，61，56，76，66，78，72，82，63，100.
（1）90分及以上为A级，75-89分为B级，60-74分为C级，60分以下为D级，请把下面表格补充完整，并将图中的条形图补充完整；
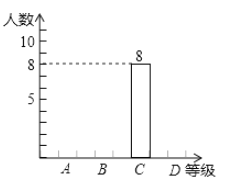
等级 | A | B | C | D |
人数 | 8 |
（2）该校七年级共有1000名学生，如果60分以上为合格，请估计七年级有多少人合格？
（3）请选择合适的统计图表示出抽测中每一个等级的人数占总人数的百分比.
