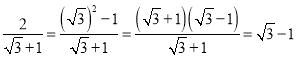题目内容
【题目】如图,AB切⊙O于点B,OA交⊙O于C点,过C作DC⊥OA交AB于D,且BD:AD=1:2.
(1)求∠A的正切值;
(2)若OC=1,求AB及![]() 的长.
的长.

【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)易知DB、DC都是⊙O的切线,由切线长定理可得DB=DC,那么结合已知条件则有:DC:AD=1:2;即Rt△ACD中,sinA=![]() ,由此可求出∠A的度数,进而可的∠A的正切值.
,由此可求出∠A的度数,进而可的∠A的正切值.
(2)连接OB.在构建的含30°角的Rt△OBA中,已知了OB=OC=1,可求出AB的长及∠BOC的度数;进而可根据弧长公式求出弧BC的长.
试题解析:(1)∵DC⊥OA,OC为半径且点C在⊙O外端,
∴DC为⊙O的切线;
∵AB为⊙O的切线,∴DC=DB;
在Rt△ACD中,
∵sinA=![]() ,BD:AD=1:2,
,BD:AD=1:2,
∴sinA=![]() ;∴∠A=30°,
;∴∠A=30°,
∴tanA=![]() .
.
(2)连接OB;

∵AB是⊙O的切线,
∴OB⊥AB.
在Rt△AOB中,
∵tanA=![]() ,OB=1;
,OB=1;
∴AB=![]()
∵∠A=30°,
∴∠O=60°;
∴![]() 的长=
的长=![]() .
.

练习册系列答案
相关题目