题目内容
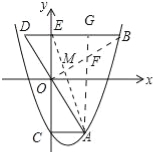
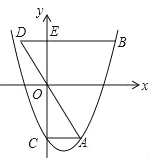
【题目】如图，抛物线y=x2﹣mx﹣3（m＞0）交y轴于点C，CA⊥y轴，交抛物线于点A，点B在抛物线上，且在第一象限内，BE⊥y轴，交y轴于点E，交AO的延长线于点D，BE=2AC．
（1）用含m的代数式表示BE的长．
（2）当m=
时，判断点D是否落在抛物线上，并说明理由．
（3）若AG∥y轴，交OB于点F，交BD于点G．
①若△DOE与△BGF的面积相等，求m的值．
②连结AE，交OB于点M，若△AMF与△BGF的面积相等，则m的值是 ．
【答案】（1）2m；（2）落在抛物线上；（3）①、m=
；②、m=
【解析】
试题分析：（1）根据A、C两点纵坐标相同，求出点A横坐标即可解决问题；（2）求出点D坐标，然后判断即可；（3）①首先根据EO=2FG，证明BG=2DE，列出方程即可解决问题；②求出直线AE、BO的解析式，求出交点M的横坐标，列出方程即可解决问题．
试题解析：（1）∵C（0，﹣3），AC⊥OC， ∴点A纵坐标为-3， y=-3时 -3=x2﹣mx-3，解得x=0或m，
∴点A坐标（m，﹣3）， ∴AC=m， ∴BE=2AC=2m．
（2）∵m=
， ∴点A坐标（
，﹣3）， ∴直线OA为y=﹣x， ∴抛物线解析式为y=x2﹣x﹣3，
∴点B坐标（2，3）， ∴点D纵坐标为3， 对于函数y=﹣x，当y=3时，x=﹣，
∴点D坐标（﹣，3）． ∵对于函数y=x2﹣x﹣3，x=﹣时，y=3，
∴点D在落在抛物线上．
（3）①∵∠ACE=∠CEG=∠EGA=90°， ∴四边形ECAG是矩形， ∴EG=AC=BG， ∵FG∥OE，
∴OF=FB，∵EG=BG， ∴EO=2FG， ∵
DEEO=GBGF， ∴BG=2DE， ∵DE∥AC， ∴
=
=，
∵点B坐标（2m，2m2﹣3）， ∴OC=2OE， ∴3=2（2m2﹣3），∵m＞0， ∴m=
．
②∵A（m，﹣3），B（2m，2m2﹣3），E（0，2m2﹣3），
∴直线AE解析式为y=﹣2mx+2m2﹣3，直线OB解析式为y=
x，
由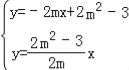
消去y得到﹣2mx+2m2﹣3=x，解得x=
，
∴点M横坐标为， ∵△AMF的面积=△BFG的面积，
∴
（
+3）（m﹣
）=m（2m2﹣3）， 整理得到：2m4﹣9m2=0， ∵m＞0，
∴m=
．
