题目内容
自然数n满足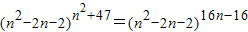 ,这样的n的个数是( )
,这样的n的个数是( )A.2
B.1
C.3
D.4
【答案】分析:分类讨论:①n2-2n-2=1;②n2-2n-2=-1;③n2-2n-2≠±1.
解答:解:①当 n2-2n-2=1 时,无论指数为何值等式成立.
解方程得 n1=3,n2=-1(不合题意,舍去);
②当 n2-2n-2=-1 时,n不为自然数;
③当 n2-2n-2≠±1 时,当n为自然数,则 n2-2n-2≠0,所以n2+47=16n-16等式成立.
解方程得 n1=7,n2=9.
综上所述,满足条件的n值有3个,故选C.
点评:此题从底数和指数两个方面分类综合考虑问题,考查学生严谨的思维能力.
解答:解:①当 n2-2n-2=1 时,无论指数为何值等式成立.
解方程得 n1=3,n2=-1(不合题意,舍去);
②当 n2-2n-2=-1 时,n不为自然数;
③当 n2-2n-2≠±1 时,当n为自然数,则 n2-2n-2≠0,所以n2+47=16n-16等式成立.
解方程得 n1=7,n2=9.
综上所述,满足条件的n值有3个,故选C.
点评:此题从底数和指数两个方面分类综合考虑问题,考查学生严谨的思维能力.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
自然数n满足(n2-2n-2)n2+47=(n2-2n-2)16n-16,这样的n的个数是( )
| A、2 | B、1 | C、3 | D、4 |
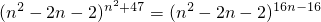 ,这样的n的个数是
,这样的n的个数是