题目内容
【题目】在平面直角坐标系xOy中,对“隔离直线”给出如下定义:
点P(x,m)是图形G1上的任意一点,点Q(x,n)是图形G2上的任意一点,若存在直线l:kx+b(k≠0)满足m≤kx+b且n≥kx+b,则称直线l:y=kx+b(k≠0)是图形G1与G2的“隔离直线”.
如图,直线l:y=-x-4是函数y=![]() (x<0)的图象与正方形OABC的一条“隔离直线”.
(x<0)的图象与正方形OABC的一条“隔离直线”.
(1)在直线y1=-2x,y2=3x+1,y3=-x+3中,是如图函数y=![]() (x<0)的图象与正方形OABC的“隔离直线”的为y1=-2x;
(x<0)的图象与正方形OABC的“隔离直线”的为y1=-2x;
请你再写出一条符合题意的不同的“隔离直线”的表达式:y=-3x;
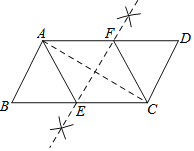
(2)如图,第一象限的等腰直角三角形EDF的两腰分别与坐标轴平行,直角顶点D的坐标是(![]() ,1),⊙O的半径为2.是否存在△EDF与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式;若不存在,请说明理由;
,1),⊙O的半径为2.是否存在△EDF与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式;若不存在,请说明理由;
(3)正方形A1B1C1D1的一边在y轴上,其它三边都在y轴的右侧,点M(1,t)是此正方形的中心.若存在直线y=2x+b是函数y=x2-2x-3(0≤x≤4)的图象与正方形A1B1C1D1的“隔离直线”,请直接写出t的取值范围.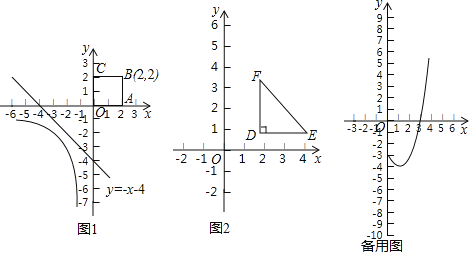
【答案】(1)y1=-2x,y=-3x;(2)y=-![]() x+4;(3)当t≥2或t≤-8时,直线y=2x+b是函数y=x2-2x-3(0≤x≤4)的图象与正方形A1B1C1D1的“隔离直线”.
x+4;(3)当t≥2或t≤-8时,直线y=2x+b是函数y=x2-2x-3(0≤x≤4)的图象与正方形A1B1C1D1的“隔离直线”.
【解析】
(1)根据的“隔离直线”的定义即可解决问题;
(2)连接OD,过点D作DG⊥x轴于点G,如图.过点D作DH⊥OD交y轴于点H,易知直线DH是⊙O的切线,也是△EDF与⊙O的“隔离直线”,求出直线DH即可解决问题;
(3)分两种情形正方形在x轴上方以及在x轴下方时,分别求出正方形的一个顶点在直线y=2x+b上时的t的值即可解决问题.
解:(1)根据的“隔离直线”的定义可知y1=-2x,是图1函数y=![]() (x<0)的图象与正方形OABC的“隔离直线”,
(x<0)的图象与正方形OABC的“隔离直线”,
直线y=-3x也是图1函数y=![]() (x<0)的图象与正方形OABC的“隔离直线”,
(x<0)的图象与正方形OABC的“隔离直线”,
故答案为y1=-2x,y=-3x.
(2)连接OD,过点D作DG⊥x轴于点G,如图.
在Rt△DGO中,OD=![]() ,
,![]()
∴∠1=30°,∠2=60°,
∵⊙O的半径为2,
∴点D在⊙O上.
过点D作DH⊥OD交y轴于点H,
∴直线DH是⊙O的切线,也是△EDF与⊙O的“隔离直线”.
在Rt△ODH中,OH=![]()
∴点H的坐标是(0,4),
∴直线DH的表达式为y=-![]() x+4,
x+4,
即所求“隔离直线”的表达式为y=-![]() x+4.
x+4.
(3)如图,
由题意F(4,5),当直线y=2x+b经过点F时,5=8+b,
∴b=-3,
∴直线y=2x-3,即图中直线EF,
∵正方形A1B1C1D1的中心M(1,t),
易知正方形正方形A1B1C1D1的边长为2,
当x=2时,y=1,
∴C1(2,1),直线EF是函数y=x2-2x-3(0≤x≤4)的图象与正方形A1B1C1D1的“隔离直线”,此时t=2,
当直线y=2x+b与y=x2-2x-3只有一个交点时,
![]()
消去y得到x2-4x-3+b=0,
由△=0,可得16-4(-3-b)=0,
解得b=-7,
此时易知M(1,-8),t=-8,
根据图象可知,当t≥2或t≤-8时,直线y=2x+b是函数y=x2-2x-3(0≤x≤4)的图象与正方形A1B1C1D1的“隔离直线”.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … |
|
|
| 0 |
| 1 |
| 2 |
| 3 | 4 | … |
y | … |
|
|
| 2 |
| 4 |
| 2 |
|
| m | … |
表中m的值为________________;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数![]() 的大致图象;
的大致图象;
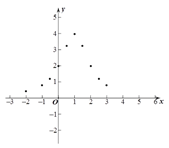
(4)结合函数图象,请写出函数![]() 的一条性质:______________________.
的一条性质:______________________.
(5)解决问题:如果函数![]() 与直线y=a的交点有2个,那么a的取值范围是______________ .
与直线y=a的交点有2个,那么a的取值范围是______________ .
【题目】顺义区某中学举行春季运动会,初二年级决定从本年级300名女生中挑选64人组成花束方队,要求身高基本一致,这个工作交给年级学生会体育部小红、小冬和小芳来完成.
为了达到年级的选拔要求,小红、小冬和小芳各自对本学校初二年级的女生身高进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1 小红抽样调查初二年级4名女同学身高统计表(单位:![]() )
)
序号 | 1 | 2 | 3 | 4 |
身高 | 155 | 160 | 165 | 172 |
表2小冬抽样调查初二年级15名女同学身高统计表(单位:![]() )
)
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
身高 | 148 | 149 | 150 | 152 | 152 | 160 | 160 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 175 |
表3小芳抽样调查初二年级15名女同学身高统计表(单位:![]() )
)
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
身高 | 145 | 160 | 150 | 152 | 160 | 154 | 160 | 166 | 167 | 168 | 160 | 169 | 173 | 174 | 175 |
根据自己的调查数据,小红说应选取身高为163![]() (数据的平均数)的同学参加方队,小冬说应选取身高为165
(数据的平均数)的同学参加方队,小冬说应选取身高为165![]() (数据的中位数)的同学参加方队,小芳说应选取身高为160
(数据的中位数)的同学参加方队,小芳说应选取身高为160![]() (数据的众数)的同学参加方队.根据以上材料回答问题:
(数据的众数)的同学参加方队.根据以上材料回答问题:
小红、小冬和小芳三人中,哪一位同学的抽样调查及得出的结论更符合年级的要求,并简要说明符合要求的理由,同时其他两位同学的抽样调查或得出结论的不足之处.