题目内容
【题目】已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.
(1)求二次函数的解析式;
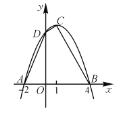
(2)设此二次函数图象的顶点为C,与y轴交点为D,求四边形ABCD的面积.
【答案】(1)、y=-![]() +2x+8;(2)、30.
+2x+8;(2)、30.
【解析】
试题分析:(1)、根据交点和最值得出顶点坐标,然后将解析式设成顶点式,然后将交点代入求出a的值;(2)、将四边形的面积转化成△AOD的面积+四边形DOEC的面积+△BCE的面积进行求解.
试题解析:(1)、由抛物线的对称性知,它的对称轴是x=1. 又∵函数的最大值为9,
∴抛物线的顶点为C(1,9). 设抛物线的解析式为y=a![]() +9,代入B(4,0),求得a=-1.
+9,代入B(4,0),求得a=-1.
∴二次函数的解析式是y=-![]() +9, 即y=-
+9, 即y=-![]() +2x+8.
+2x+8.
(2)、

当x=0时,y=8,即抛物线与y轴的交点坐标为D(0,8).
过C作CE⊥x轴于E点.
∴S四边形ABCD=S△AOD+S四边形DOEC+S△BCE=![]() ×2×8+
×2×8+![]() ×(8+9)×1+
×(8+9)×1+![]() ×3×9=30.
×3×9=30.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目