Question

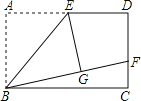
【题目】如图，矩形ABCD中，E是AD的中点，将△ABE沿直线BE折叠后得到△GBE，延长BG交CD于点F．若AB=6，BC=10，则FD的长为（ ）

A． B．4 C． D．5

Answer 1

【答案】C

【解析】

试题分析：根据点E是AD的中点以及翻折的性质可以求出AE=DE=EG，然后利用“HL”证明△EDF和△EGF全等，根据全等三角形对应边相等可证得DF=GF；设FD=x，表示出FC、BF，然后在Rt△BCF中，利用勾股定理列式进行计算即可得解．

解：∵E是AD的中点，

∴AE=DE，

∵△ABE沿BE折叠后得到△GBE

∴AE=EG，AB=BG，

∴ED=EG，

∵在矩形ABCD中，

∴∠A=∠D=90°，

∴∠EGF=90°，

∵在Rt△EDF和Rt△EGF中，

，

∴Rt△EDF≌Rt△EGF（HL），

∴DF=FG，

设DF=x，则BF=6+x，CF=6﹣x，

在Rt△BCF中，102+（6﹣x）2=（6+x）2，

解得x=．

故选：C．