��Ŀ����
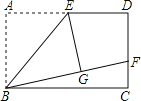
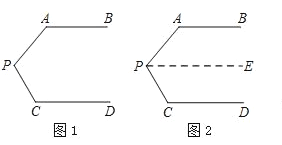
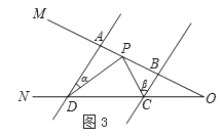
����Ŀ�������龳����ͼ1��AB��CD����PAB=130�㣬��PCD=120�㣮����APC������
С���Ľ���˼·�ǣ���ͼ2����P��PE��AB��ͨ��ƽ�������ʣ��ɵ���APC=50��+60��=110�㣮
����Ǩ�ƣ�
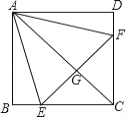
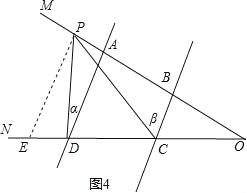
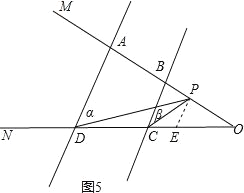
��1����ͼ3��AD��BC����P������OM���˶�������P��A��B����֮���˶�ʱ����ADP=��������BCP=���£����ж���CPD������������֮���к�������ϵ����˵�����ɣ�
��2���ڣ�1���������£������P��A��B��������˶�ʱ����P���A��B��O���㲻�غϣ�������ֱ��д����CPD�����������¼��������ϵ��
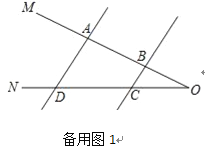
���𰸡���1����CPD=����+���£����ɼ�������
��2����P��BA�ӳ���ʱ����CPD=���©���������P��AB�ӳ���ʱ����CPD=���������£�
�����������������(1)��������P��PE��AD��CD��E��Ȼ�����ƽ���ߵ����ʵó�����=��DPE������=��CPE���Ӷ��ó�����Ĵ𰸣�(2)�����ݵ�һ��ͬ���ķ����ó��Ƕ�֮��Ĺ�ϵ���Ӷ��ó���.
�����������1���⣺��CPD=����+���£��������£�
��ͼ3����P��PE��AD��CD��E��
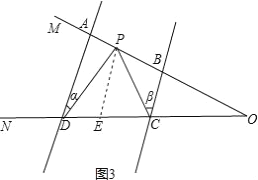
��AD��BC�� ��AD��PE��BC�� �����=��DPE������=��CPE��
���CPD=��DPE+��CPE=����+���£�
��2����P��BA�ӳ���ʱ����CPD=���©�������
��P��AB�ӳ���ʱ�� ��CPD=���������£�

����Ŀ��ʵʩ���ʽ���������ij��ѧ������ѧ����������չ�����������γ���Դ�������꼶������������ѧϰС�飬���������꼶ѧ���μ�����ѧϰС���ͳ�Ʊ�������ͳ��ͼ���������ͼ�����ṩ����Ϣ�ش��������⣮
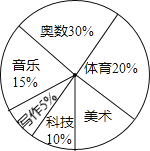
ѧϰС�� | ���� | ���� | �Ƽ� | ���� | д�� | ���� |
���� | 72 | 36 | 54 | 18 |
��1�����꼶����ѧ�� �ˣ�
��2���ڱ����еĿո�������Ӧ�����֣�
��3�����������ṩ���������ݵ���λ���� ��
��4�������� ��