Question

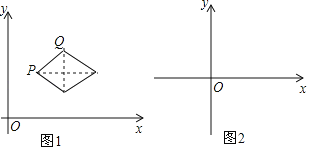
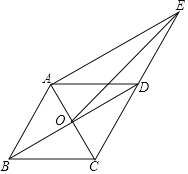
【题目】如图，平行四边形ABCD的对角线AC，BD相交于点O，延长CD到E，使DE＝CD，连接AE．

（1）求证：四边形ABDE是平行四边形；

（2）连接OE，若∠ABC＝60°，且AD＝DE＝4，求OE的长．

Answer 1

【答案】(1)见解析;(2)2.

【解析】

(1)四边形ABCD是平行四边形，由平行四边形的性质，可得AB=DE， AB//DE ，则四边形ABDE是平行四边形；

(2)因为AD=DE=4，则AD=AB=4，四边形ABCD是菱形，由菱形的性质及解直角三角形可得AO=ABsin∠ABO=2，BO=ABcos∠ABO=2， BD=4 ，则AE=BD，利用勾股定理可得OE．

（1）证明：∵四边形ABCD是平行四边形，

∴AB∥CD，AB＝CD．

∵DE＝CD，

∴AB＝DE．

∴四边形ABDE是平行四边形；

（2）∵AD＝DE＝4，

∴AD＝AB＝4．

∴ABCD是菱形，

∴AB＝BC，AC⊥BD，，．

又∵∠ABC＝60°，

∴∠ABO＝30°．

在Rt△ABO中，，．

∴．

∵四边形ABDE是平行四边形，

∴AE∥BD，．

又∵AC⊥BD，

∴AC⊥AE．

在Rt△AOE中，．