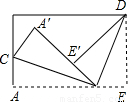
题目内容
 将一矩形纸片按图的方式折叠,BC、BD为折痕,折叠后A′B与E′B在同一条直线上,则下列结论中,不一定正确的是
将一矩形纸片按图的方式折叠,BC、BD为折痕,折叠后A′B与E′B在同一条直线上,则下列结论中,不一定正确的是
- A.∠CBD=90°
- B.DE′⊥A′B
- C.△A′BC≌△E′DB
- D.△ABC≌△A′BC
C
分析:根据翻折变换的特点可知,∠CBD=90°,DE′⊥A′B.但是AC,BE不一定相等,当AC≠BE时,△A′BC与△E′DB,△ABC与△EDB不会全等.
解答:A、BC平分∠ABA′,BD平分∠EBE′,所以∠CBD=90°,故选项正确;
B、∠BE′D=∠E=90°,所以DE′⊥A′B,故选项正确;
C、C不一定正确,故选项错误;
D、根据折叠的性质得到一定正确,故选项正确.
故选C.
点评:本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.
分析:根据翻折变换的特点可知,∠CBD=90°,DE′⊥A′B.但是AC,BE不一定相等,当AC≠BE时,△A′BC与△E′DB,△ABC与△EDB不会全等.
解答:A、BC平分∠ABA′,BD平分∠EBE′,所以∠CBD=90°,故选项正确;
B、∠BE′D=∠E=90°,所以DE′⊥A′B,故选项正确;
C、C不一定正确,故选项错误;
D、根据折叠的性质得到一定正确,故选项正确.
故选C.
点评:本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 6、将一矩形纸片按如图方式折叠,BC、BD为折痕,折叠后A′B与E′B在同一条直线上,则∠CBD的度数( )
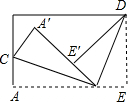
6、将一矩形纸片按如图方式折叠,BC、BD为折痕,折叠后A′B与E′B在同一条直线上,则∠CBD的度数( )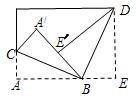 9、将一矩形纸片按图的方式折叠,BC、BD为折痕,折叠后A′B与E′B在同一条直线上,则下列结论中,不一定正确的是( )
9、将一矩形纸片按图的方式折叠,BC、BD为折痕,折叠后A′B与E′B在同一条直线上,则下列结论中,不一定正确的是( )