题目内容
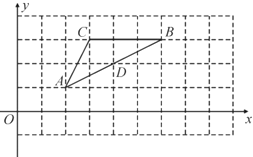
【题目】二次函数![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() ,与直线
,与直线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 在
在![]() 轴上,
轴上,![]() .
.
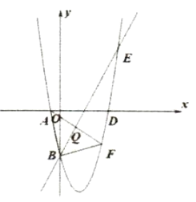
(1)求二次函数的解析式;
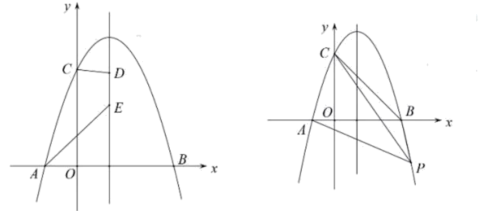
(2)在抛物线上有一点![]() ,若
,若![]() 的面积为
的面积为![]() ,求点
,求点![]() 的横坐标;
的横坐标;
(3)点![]() 在第四象限的抛物线上运动,连接
在第四象限的抛物线上运动,连接![]() ,与直线
,与直线![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() .设
.设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)点P的横坐标为
;(2)点P的横坐标为![]() ,
,![]() ,
,![]() 或7;(3)
或7;(3)![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)先求出n的值,然后把点D、E代入二次函数,即可求出二次函数的解析式;
(2)先求出点A的坐标,然后得到直线AE的解析式和AE的长度,然后求出![]() 的高PF的长度,作直线AE的平行线,使得平行线之间的距离为
的高PF的长度,作直线AE的平行线,使得平行线之间的距离为![]() ,分别求出两条直线,联合抛物线的解析式,即可求出点P的坐标;
,分别求出两条直线,联合抛物线的解析式,即可求出点P的坐标;
(3)先求出直线AF的解析式,联合直线BE得到点Q的横坐标,过点Q作QM⊥x轴,作FN⊥x轴,则有QM∥FN,得到AM和MN的值,由平行线分线段成比例,则![]() ,结合二次函数的性质,即可得到答案.
,结合二次函数的性质,即可得到答案.
解:(1)把点E代入直线![]() ,则
,则
![]() ,
,
∴点E为(6,7),
把点![]() ,E(6,7)代入
,E(6,7)代入![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴二次函数的解析式为:![]() ;
;
(2)∵![]() ,
,
令![]() ,
,
∴![]() ,
,![]() ,
,
∴点A为(![]() ,0),
,0),
∵点E为(6,7),
∴AE=![]() ,
,
∴直线AE为:![]() ;
;
∵点P在抛物线上,且![]() 的面积为
的面积为![]() ,
,
∴![]() ,
,
∴![]() ;
;
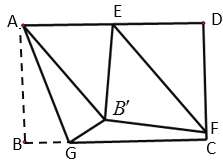
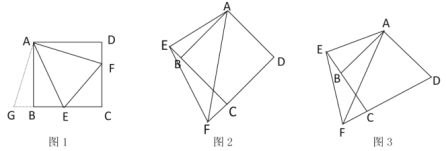
如图,作直线AE的平行线,使得平行线之间的距离为![]() ,
,
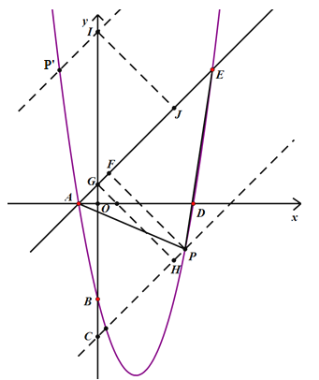
∵![]() ,
,
∴∠EAD=45°,
∴△CGH和△GIJ是等腰直角三角形,
∴GI=GC=8;
∵直线AE为![]() ,
,
∴直线CP为![]() ;直线
;直线![]() 为
为![]() ;
;
联合方程组,得
![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
∴点P的横坐标为![]() ,
,![]() ,
,![]() 或7;
或7;
(3)∵点F在抛物线![]() 上,则
上,则
设点F为(t,![]() ),
),
∵点A为(![]() ,0),
,0),
设直线AF为![]() ,则
,则
![]() ,
,
即![]() ,
,
∵点F在第四象限,则![]() ,
,
∴![]() ,
,
∴直线AF为![]() ;
;
∵直线BE为![]() ,
,
则![]() ,解得:
,解得:![]() ,
,
∴点Q的横坐标为![]() ;
;
如图,过点Q作QM⊥x轴,作FN⊥x轴,则有QM∥FN,
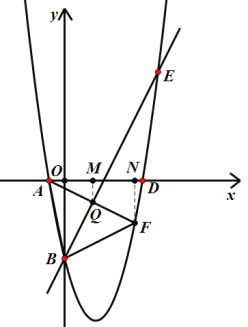
∴![]() ,
,
∵点M为(![]() ,0),点N为(t,0),
,0),点N为(t,0),
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴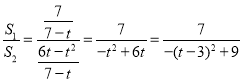 ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() 有最大值9,则此时
有最大值9,则此时![]() 有最小值;
有最小值;
∴![]() 的最小值为
的最小值为![]() .
.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案