Question

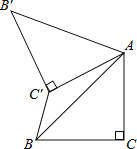
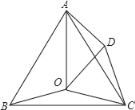
【题目】如图，点O是等边三角形ABC内的一点，∠BOC＝150°，将△BOC绕点C按顺时针旋转得到△ADC，连接OD，OA．

（1）求∠ODC的度数；

（2）若OB＝2，OC＝3，求AO的长．

Answer 1

【答案】（1）60°；（2）

【解析】

（1）根据旋转的性质得到三角形ODC为等边三角形即可求解；

（2）在Rt△AOD中，由勾股定理即可求得AO的长．

（1）由旋转的性质得：CD=CO，∠ACD=∠BCO．

∵∠ACB=60°，∴∠DCO=60°，∴△OCD为等边三角形，∴∠ODC=60°；

（2）由旋转的性质得：AD=OB=2．

∵△OCD为等边三角形，∴OD=OC=3．

∵∠BOC=150°，∠ODC=60°，∴∠ADO=90°．

在Rt△AOD中，由勾股定理得：AO．