Question

如图，有一底角为35°的等腰三角形纸片，现过底边上一点，沿与底边垂直的方向将其剪开，分成三角形和四边形两部分，则四边形中，最大角的度数是    度．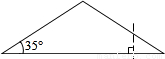

Answer 1

【答案】分析：根据等腰三角形的性质，依题意可得等腰三角形的顶角为110°，又根据三角形的一个外角等于和它不相邻的内角的和可求出最大角的度数．
解答：解：根据等腰三角形的性质：等边对等角．以及三角形的内角和是180°，解得等腰三角形的顶角是180°-35°×2=110°．根据三角形的一个外角等于和它不相邻的内角的和求得四边形的第四个角是90°+35°=125°．比较四边形的四个内角，最大角的度数是125°．
故填125．
点评：本题考查了等腰三角形的性质、三角形的内角和定理和三角形的外角性质；利用三角形外角的性质求得四边形的内角后与其它三个角进行比较式正确解答本题的关键．