题目内容
【题目】如图,直线m的表达式为y =﹣3x+3,且与x轴交于点B,直线n经过点A(4,0),且与直线m交于点C(t,﹣3)
(1)求直线n的表达式.
(2)求△ABC的面积.
(3)在直线n上存在异于点C的另一点P,使△ABP与△ABC的面积相等,请直接写出点P的坐标是 .
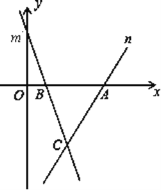
【答案】(1)n的表达式为![]() ;(2)S△ABC的面积是4.5;(3)P点坐标为(6,3).
;(2)S△ABC的面积是4.5;(3)P点坐标为(6,3).
【解析】
(1)把C点坐标代入直线m,可求得t,再由待定系数法可求得直线n的解析式;
(2)可先求得B点坐标,则可求得AB,再由C点坐标可求得△ABC的面积;
(3)由面积相等可知点P到x轴的距离和点C到y轴的距离相等,可求得P点纵坐标,代入直线n的解析式可求得P点坐标.
(1)∵直线m过C点,
∴-3=-3t+3,解得t=2,
∴C(2,-3),
设直线n的解析式为y=kx+b,
把A、C两点坐标代入可得
![]() ,
,
解得![]() ,
,
∴直线n的解析式为y=1.5x-6;
(2)在y=-3x+3中,令y=0,可得0=-3x+3,解得x=1,
∴B(1,0),且A(4,0),
∴AB=4-1=3,且C点到x轴的距离h=3,![]() ∴S△ABC=
∴S△ABC=
(3)由点P在直线n上,故可设P点坐标为(x,1.5x-6),
∵S△ABC=S△ABP,
∴P到x轴的距离=3,
∵C、P两点不重合,
∴P点的纵坐标为3,
∴1.5x-6=3,解得x=6,
∴P点坐标为(6,3).

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目