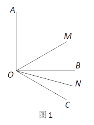题目内容
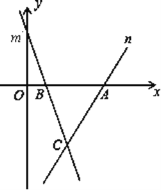
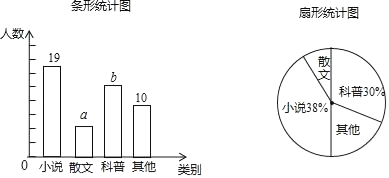
【题目】![]() 操作思考:如图1,在平面直角坐标系中,等腰
操作思考:如图1,在平面直角坐标系中,等腰![]() 的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点
的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点![]() 处
处![]() 则
则![]() 的长为______;
的长为______;![]() 点B的坐标为______
点B的坐标为______![]() 直接写结果
直接写结果![]()
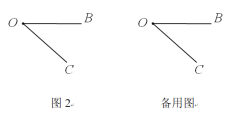
![]() 感悟应用:如图2,在平面直角坐标系中,将等腰
感悟应用:如图2,在平面直角坐标系中,将等腰![]() 如图放置,直角顶点
如图放置,直角顶点![]() ,点
,点![]() ,试求直线AB的函数表达式.
,试求直线AB的函数表达式.
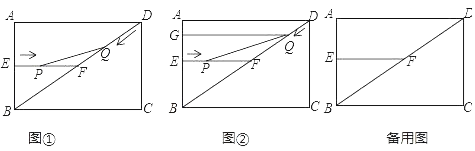
![]() 拓展研究:如图3,在直角坐标系中,点
拓展研究:如图3,在直角坐标系中,点![]() ,过点B作
,过点B作![]() 轴,垂足为点A,作
轴,垂足为点A,作![]() 轴,垂足为点C,P是线段BC上的一个动点,点Q是直线
轴,垂足为点C,P是线段BC上的一个动点,点Q是直线![]() 上一动点
上一动点![]() 问是否存在以点P为直角顶点的等腰
问是否存在以点P为直角顶点的等腰![]() ,若存在,请求出此时P的坐标,若不存在,请说明理由.
,若存在,请求出此时P的坐标,若不存在,请说明理由.
【答案】(1)![]() ,
,![]() (2)
(2)![]() (3)
(3)![]() ,
,![]()
【解析】
![]() 由
由![]() 可得,
可得,![]() ,
,![]() ,
,![]() ,易证
,易证![]() ≌
≌![]() ,
,![]() ,
,![]() ,因此
,因此![]() ;
;
![]() 同
同![]() 可证
可证![]() ≌
≌![]() ,
,![]() ,
,![]() ,
,![]() ,求得
,求得![]() 最后代入求出一次函数解析式即可;
最后代入求出一次函数解析式即可;
![]() 分两种情况讨论
分两种情况讨论![]() 当点Q在x轴下方时,
当点Q在x轴下方时,![]() 当点Q在x轴上方时
当点Q在x轴上方时![]() 根据等腰
根据等腰![]() 构建一线三直角,从而求解.
构建一线三直角,从而求解.
![]() 如图1,作
如图1,作![]() 轴,
轴,![]() 轴.
轴.
![]() ,
,
![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
故答案为![]() ,
,![]() ;
;
![]() 如图2,过点B作
如图2,过点B作![]() 轴.
轴.
![]() ,
,![]()
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() .
.
设直线AB的表达式为![]()
将![]() 和
和![]() 代入,得
代入,得
![]() ,
,
解得 ,
,
![]() 直线AB的函数表达式
直线AB的函数表达式![]() .
.
![]() 如图3,设
如图3,设![]() ,分两种情况:
,分两种情况:
![]() 当点Q在x轴下方时,
当点Q在x轴下方时,![]() 轴,与BP的延长线交于点
轴,与BP的延长线交于点![]() .
.
![]() ,
,
![]() ,
,
![]()
在![]() 与
与![]() 中
中

![]() ≌
≌![]()
![]() ,
,![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
解得![]()
![]()
此时点P与点C重合,
![]() ;
;
![]() 当点Q在x轴上方时,
当点Q在x轴上方时,![]() 轴,与PB的延长线交于点
轴,与PB的延长线交于点![]() .
.
同理可证![]() ≌
≌![]() .
.
同理求得![]()
综上,P的坐标为:![]() ,
,![]()

练习册系列答案
相关题目
【题目】小明上周零花钱使用情况:(规定:超过50元记为正,少于50元记为负)
星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
+11 | +10 | ﹣17 | +18 | ﹣12 |
请你解答以下问题:
(1)上星期五小明用了多少零花钱;
(2)上星期四比上星期三多花了多少零花钱;
(3)求上周平均每天用多少钱?