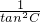题目内容
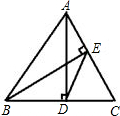如图，AD、BE是锐角△ABC的两条高，则△CDE与△ABC的面积比等于（ ）| A、sin2C | ||
| B、cos2C | ||
| C、tan2C | ||
D、
|
分析：先由∠CDA=∠CEB，∠C=∠C证△CDA和△CEB相似，由此得到比例式
=
，再证△CDE和△CAB相似，根据相似三角形的面积之比等于相似比的平方即可得出选项．
| CD |
| AC |
| CE |
| BC |
解答：解：∵AD、BE是锐角△ABC的两条高，
∴∠CDA=∠CEB=90°，
∵∠C=∠C，
∴△CDA∽△CEB，
∴
=
，
即：
=
，
在△CDE∽△CAB中，
∵
=
，∠C=∠C，
∴△CDE∽△CAB，ADC中
∴
=(
)2，
在△ADC中，cosC=
，
∴
=cos2C．
故选B．
∴∠CDA=∠CEB=90°，
∵∠C=∠C，
∴△CDA∽△CEB，
∴
| CD |
| CE |
| AC |
| BC |
即：
| CD |
| AC |
| CE |
| BC |
在△CDE∽△CAB中，
∵
| CD |
| AC |
| CE |
| BC |
∴△CDE∽△CAB，ADC中
∴
| S△CDE |
| S△CAB |
| CD |
| CA |
在△ADC中，cosC=
| CD |
| CA |
∴
| S△CDE |
| S△CAB |
故选B．
点评：本题主要考查了三角形的面积公式，相似三角形的性质和判定，直角三角形的性质等知识点，灵活运用相似三角形的性质和判定是解此题的关键．
练习册系列答案
相关题目
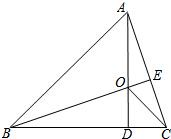10、如图，AD、BE是锐角△ABC的高，相交于点O，若BO=AC，BC=7，CD=2，则AO的长为（ ）
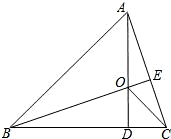如图，AD、BE是锐角△ABC的高，相交于点O，若BO=AC，BC=7，CD=2，则AO的长为
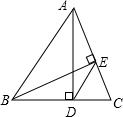如图，AD、BE是锐角三角形的两条高，S△ABC=18，S△DEC=2，则cosC等于
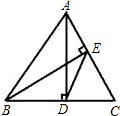如图，AD、BE是锐角△ABC的两条高，则△CDE与△ABC的面积比等于