题目内容
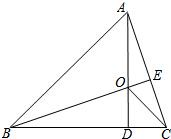 10、如图,AD、BE是锐角△ABC的高,相交于点O,若BO=AC,BC=7,CD=2,则AO的长为( )
10、如图,AD、BE是锐角△ABC的高,相交于点O,若BO=AC,BC=7,CD=2,则AO的长为( )分析:由AD、BE是锐角△ABC的高,可得∠DBA=∠DAC,又BO=AC,∠BDO=∠ADC=90°,故△BDO≌△ADC,可得BD=AD,DO=CD,再由边的关系即可求出AO的长.
解答:解:∵AD、BE是锐角△ABC的高
∴∠DBA=∠DAC
∵BO=AC,∠BDO=∠ADC=90°
∴△BDO≌△ADC
∴BD=AD,DO=CD
∵BD=BC-CD=5
∴AD=5
∴AO=AD-OD=AD-CD=3
故此题应选B项.
∴∠DBA=∠DAC
∵BO=AC,∠BDO=∠ADC=90°
∴△BDO≌△ADC
∴BD=AD,DO=CD
∵BD=BC-CD=5
∴AD=5
∴AO=AD-OD=AD-CD=3
故此题应选B项.
点评:本题考查了全等三角形的判定和性质;结合已知条件发现并利用△BDO≌△ADC是正确解答本题的关键.

练习册系列答案
相关题目
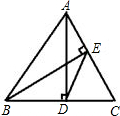 如图,AD、BE是锐角△ABC的两条高,则△CDE与△ABC的面积比等于( )
如图,AD、BE是锐角△ABC的两条高,则△CDE与△ABC的面积比等于( )| A、sin2C | ||
| B、cos2C | ||
| C、tan2C | ||
D、
|
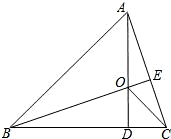 如图,AD、BE是锐角△ABC的高,相交于点O,若BO=AC,BC=7,CD=2,则AO的长为
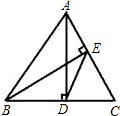
如图,AD、BE是锐角△ABC的高,相交于点O,若BO=AC,BC=7,CD=2,则AO的长为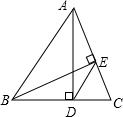 如图,AD、BE是锐角三角形的两条高,S△ABC=18,S△DEC=2,则cosC等于
如图,AD、BE是锐角三角形的两条高,S△ABC=18,S△DEC=2,则cosC等于


 如图,AD、BE是锐角△ABC的两条高,则△CDE与△ABC的面积比等于
如图,AD、BE是锐角△ABC的两条高,则△CDE与△ABC的面积比等于