题目内容
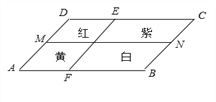
【题目】如图,一个四边形花坛ABCD,被两条线段MN,EF分成四个部分,分别种上红、黄、紫、白四种花卉,种植面积依次是S1,S2,S3,S4,若MN∥AB∥CD,EF∥DA∥CB,则有( )
A. S1=S4 B. S1+S4=S2+S3 C. S1S4=S2S3 D. 都不对
【答案】C
【解析】设红、紫四边形的高相等为h1,黄、白四边形的高相等,高为h2,
则S1=DEh1,S2=AFh2,S3=ECh1,S4=FBh2,
因为DE=AF,EC=FB,所以A不对;
S1+S4=DEh1+FBh2=AFh1+FBh2,
S2+S3=AFh2+ECh1=AFh2+FBh1,
所以B不对;
S1S4=DEh1FBh2=AFh1FBh2,
S2S3=AFh2ECh1=AFh2FBh1,
所以S1S4=S2S3,
故选C。

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目