题目内容
正六边形的边长为2cm,则它的面积为分析:根据题意画出图形,由正六边形的特点求出∠AOB的度数及OG的长,再由△OAB的面积即可求解.
解答: 解:∵此多边形为正六边形,
解:∵此多边形为正六边形,
∴∠AOB=
=60°;
∵OA=OB,
∴△OAB是等边三角形,
∴OA=AB=2cm,
∴OG=OA•cos30°=2×
=
,
∴S△OAB=
×AB×OG=
×2×
=
cm,
∴S六边形=6S△OAB=6×
=6
cm.
 解:∵此多边形为正六边形,
解:∵此多边形为正六边形,∴∠AOB=
| 360° |
| 6 |
∵OA=OB,
∴△OAB是等边三角形,
∴OA=AB=2cm,
∴OG=OA•cos30°=2×
| ||
| 2 |
| 3 |
∴S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴S六边形=6S△OAB=6×
| 3 |
| 3 |
点评:此题主要考查正多边形的计算问题,属于常规题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
已知正六边形的边心距为
,则正六边形的边长为( )
| 3 |
A、2
| ||
| B、2 | ||
| C、1 | ||
D、
|
 ,则正六边形的边长为
,则正六边形的边长为 ,则cosβ=
,则cosβ= ;
; :1;
:1;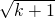 x+1=0有两个不相等的实数根,则k的取值范围是k<
x+1=0有两个不相等的实数根,则k的取值范围是k< ,则正六边形的边长为( )
,则正六边形的边长为( )
