题目内容
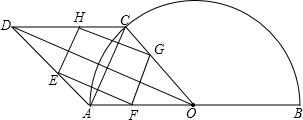
问题背景:如图,点C是半圆O上一动点(点C与A、B不重合),AB=2,连接AC、BC、OC,将△AOC沿直线AC翻折得△ADC,点、E、F、G、H分别是DA、AO、OC、CD的中点.(1)猜想证明:猜想四边形AOCD以及四边形EFGH的形状,并证明你的结论;
(2)拓展探究:探究点C在半圆弧上哪个位置时,四边形EFGH面积最大?求出这个最大值,判断此时四边形EFGH的形状,并说明理由.
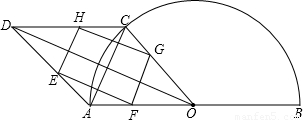
【答案】分析:(1)先根据翻折变换的性质得出AO=AD,CO=CD,由菱形的判定定理得出四边形AOCD是菱形,再根据三角形中位线定理得出FG平行且等于EH,进而可判断出四边形EFGH是矩形;
(2)根据AB为半圆O的直径得出∠ACB=90°,可判断出四边形AOCD是菱形,再根据菱形的性质及AO=OB判断出四边形OBCD是平行四边形,DO平行且等于BC,进而可求出矩形EFGH的面积,可知当点C位于半圆弧中点时,AB边上的高最大此时S△ACB的最大值为1,S矩形EFGH的最大值为 ,进而可判断出矩形EFGH是正方形.
,进而可判断出矩形EFGH是正方形.
解答:解:(1)四边形AOCD是菱形;四边形EFGH是矩形.证明如下:
由翻折可得AO=AD,CO=CD.
∵OA=OC,
∴AO=OC=CD=DA.
∴四边形AOCD是菱形;(3分)
∴AC⊥OD.
又∵EF是△AOD的中位线,
∴EF∥OD,且EF= OD,
OD,
同理可得FG∥AC,且FG= AC,EH∥AC,
AC,EH∥AC,
且EH= AC,
AC,
∴FG平行且等于EH,
∴四边形EFGH是平行四边形,且FG⊥EF,
∴四边形EFGH是矩形.(6分)
(2)∵AB为半圆O的直径,
∴∠ACB=90°.
∴AC⊥BC.
∵四边形AOCD是菱形,
∴DC平行且等于OA,
又∵AO=OB,
∴DC平行且等于OB,
∴四边形OBCD是平行四边形,
∴DO平行且等于BC,
∴S矩形EFGH=EF•EH= OD•
OD• AC=
AC= BC•AC=
BC•AC= ×S△ACB,(8分)
×S△ACB,(8分)
∴当点C位于半圆弧中点时,AB边上的高最大,
即S△ACB的最大值为1.
∴S矩形EFGH的最大值为 .此时AC=BC,
.此时AC=BC,
∴AC=OD.
∴EF=FG,
∴矩形EFGH是正方形.(10分)
点评:本题考查的是图形的翻折变换、圆周角定理、三角形的中位线定理、菱形的判定与性质、矩形的判定与性质,涉及面较广,难度较大.
(2)根据AB为半圆O的直径得出∠ACB=90°,可判断出四边形AOCD是菱形,再根据菱形的性质及AO=OB判断出四边形OBCD是平行四边形,DO平行且等于BC,进而可求出矩形EFGH的面积,可知当点C位于半圆弧中点时,AB边上的高最大此时S△ACB的最大值为1,S矩形EFGH的最大值为
 ,进而可判断出矩形EFGH是正方形.
,进而可判断出矩形EFGH是正方形.解答:解:(1)四边形AOCD是菱形;四边形EFGH是矩形.证明如下:
由翻折可得AO=AD,CO=CD.
∵OA=OC,
∴AO=OC=CD=DA.
∴四边形AOCD是菱形;(3分)
∴AC⊥OD.
又∵EF是△AOD的中位线,
∴EF∥OD,且EF=
 OD,
OD,同理可得FG∥AC,且FG=
 AC,EH∥AC,
AC,EH∥AC,且EH=
 AC,
AC,∴FG平行且等于EH,
∴四边形EFGH是平行四边形,且FG⊥EF,
∴四边形EFGH是矩形.(6分)
(2)∵AB为半圆O的直径,
∴∠ACB=90°.
∴AC⊥BC.
∵四边形AOCD是菱形,
∴DC平行且等于OA,
又∵AO=OB,
∴DC平行且等于OB,
∴四边形OBCD是平行四边形,
∴DO平行且等于BC,
∴S矩形EFGH=EF•EH=
 OD•
OD• AC=
AC= BC•AC=
BC•AC= ×S△ACB,(8分)
×S△ACB,(8分)∴当点C位于半圆弧中点时,AB边上的高最大,
即S△ACB的最大值为1.
∴S矩形EFGH的最大值为
 .此时AC=BC,
.此时AC=BC,∴AC=OD.
∴EF=FG,
∴矩形EFGH是正方形.(10分)
点评:本题考查的是图形的翻折变换、圆周角定理、三角形的中位线定理、菱形的判定与性质、矩形的判定与性质,涉及面较广,难度较大.

练习册系列答案
相关题目
 值,判断此时四边形EFGH的形状,并说明理由.
值,判断此时四边形EFGH的形状,并说明理由. (2011•临川区模拟)问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
(2011•临川区模拟)问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
 值,判断此时四边形EFGH的形状,并说明理由.
值,判断此时四边形EFGH的形状,并说明理由.