题目内容
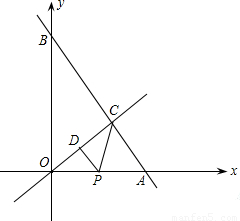
(2006•徐州)如图,已知AB是⊙O的直径,PA是⊙O的切线,过点B作BC∥OP交⊙O于点C,连接AC.(1)求证:△ABC∽△POA;
(2)若AB=2,PA=
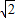 ,求BC的长.(结果保留根号)
,求BC的长.(结果保留根号)
【答案】分析:此题首先要掌握圆的性质,直径所对的圆周角是直角;根据切线的性质可得∠PAO=90°,根据平行线的性质,可得∠AOP=∠CBA,所以可证得△ABC∽△POA,根据相似三角形的性质,相似三角形的对应边成比例可求得BC的长.
解答:(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°.
∵PA是⊙O的切线,
∴∠OAP=90°.
∵BC∥OP,
∴∠AOP=∠CBA.
则△ABC∽△POA.
(2)解:∵AB是⊙O的直径,且AB=2,
∴OA=1.
∵在Rt△OAP中,PA=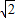 ,
,
∴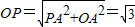 .
.
∵由(1)可知△ABC∽△POA,
∴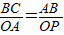 .
.
则BC=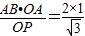 .
.
∴求得BC= .
.
点评:此题考查了相似三角形的判定和性质,①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;③如果两个三角形的两个对应角相等,那么这两个三角形相似.
解答:(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°.
∵PA是⊙O的切线,
∴∠OAP=90°.
∵BC∥OP,
∴∠AOP=∠CBA.
则△ABC∽△POA.
(2)解:∵AB是⊙O的直径,且AB=2,
∴OA=1.
∵在Rt△OAP中,PA=
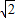 ,
,∴
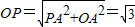 .
.∵由(1)可知△ABC∽△POA,
∴
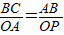 .
.则BC=
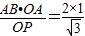 .
.∴求得BC=
 .
.点评:此题考查了相似三角形的判定和性质,①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;③如果两个三角形的两个对应角相等,那么这两个三角形相似.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目


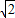 ,求BC的长.(结果保留根号)
,求BC的长.(结果保留根号)