题目内容
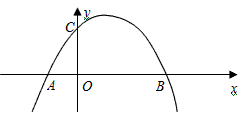
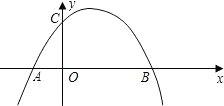
已知:如图所示,关于x的抛物线y=ax2+x+c(a≠0)与x轴交于点A(-2,0)、点B(6,0),与y轴交于点C.(1)求出此抛物线的解析式,并写出顶点坐标;
(2)在抛物线上有一点D,使四边形ABDC为等腰梯形,写出点D的坐标,并求出直线AD的解析式;
(3)在(2)中的直线AD交抛物线的对称轴于点M,抛物线上有一动点P,x轴上有一动点Q
 .是否存在以A、M、P、Q为顶点的平行四边形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
.是否存在以A、M、P、Q为顶点的平行四边形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
分析:(1)可将A,B两点的坐标代入函数的解析式中,可求出抛物线的解析式.进而求出对称轴的解析式和定点的坐标;
(2)由于二次函数和等腰梯形都是轴对称图形,可根据抛物线的对称轴和C点的坐标求出D的坐标.然后用待定系数法求出A,D所在直线的解析式.
(3)分五种情况进行讨论:
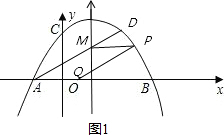
①如图1,P与M的纵坐标相等,可将M的纵坐标代入抛物线中求出P的坐标,然后可根据M,P的横坐标求出MP的长,即AQ的长,然后根据A的坐标即可求出Q的坐标.
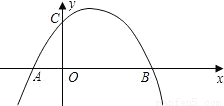
②如图2,方法同①.
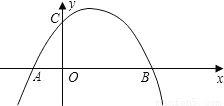
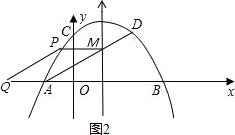
③如图3,根据平行四边形的对称性,那么M,P的纵坐标互为相反数,因此可求出P的坐标,可先在三角形AOM中求出AO的长,然后A到抛物线对称轴的长+P的横坐标=Q的横坐标,据此可求出Q点的坐标.
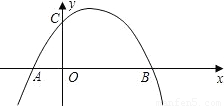
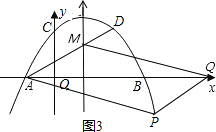
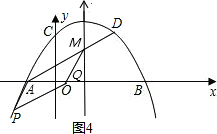
④如图4,可参照③的方法求出P的坐标,然后求出PA的长,即MQ的长,然后可过D作x轴的垂线,通过构建直角三角形求出OQ的长.进而得出Q的坐标.
⑤根据题意画出图形,即可求出答案.
(2)由于二次函数和等腰梯形都是轴对称图形,可根据抛物线的对称轴和C点的坐标求出D的坐标.然后用待定系数法求出A,D所在直线的解析式.




(3)分五种情况进行讨论:
①如图1,P与M的纵坐标相等,可将M的纵坐标代入抛物线中求出P的坐标,然后可根据M,P的横坐标求出MP的长,即AQ的长,然后根据A的坐标即可求出Q的坐标.
②如图2,方法同①.
③如图3,根据平行四边形的对称性,那么M,P的纵坐标互为相反数,因此可求出P的坐标,可先在三角形AOM中求出AO的长,然后A到抛物线对称轴的长+P的横坐标=Q的横坐标,据此可求出Q点的坐标.
④如图4,可参照③的方法求出P的坐标,然后求出PA的长,即MQ的长,然后可过D作x轴的垂线,通过构建直角三角形求出OQ的长.进而得出Q的坐标.
⑤根据题意画出图形,即可求出答案.
解答:解:(1)根据题意,得
,
解得
,
∴抛物线的解析式为y=-
x2+x+3,
顶点坐标是(2,4);
(2)D(4,3),
设直线AD的解析式为y=kx+b(k≠0),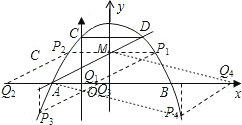
∵直线经过点A(-2,0)、点D(4,3),
∴
,
∴
,
∴y=
x+1;
(3)存在.
①如图1,P与M的纵坐标相等,可将M的纵坐标代入抛物线中求出P的坐标,然后可根据M,P的横坐标求出MP的长,即AQ的长,然后根据A的坐标即可求出Q的坐标:Q1(2
-2,0);
②如图2,方法同①,Q2(-2
-2,0);
③如图3,根据平行四边形的对称性,那么M,P的纵坐标互为相反数,因此可求出P的坐标,可先在三角形AOM中求出AO的长,然后A到抛物线对称轴的长+P的横坐标=Q的横坐标,据此可求出Q点的坐标:Q3(6-2
,0);
④如图4,可参照③的方法求出P的坐标,然后求出PA的长,即MQ的长,然后可过D作x轴的垂线,通过构建直角三角形求出OQ的长.进而得出Q的坐标:Q4(6+2
,0).
⑤以AM为对角线时,把x=2代入y=
x+1得y=2,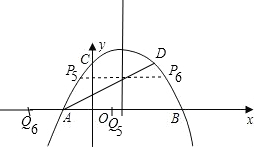
即M的坐标是(2,2),
过M作x轴的平行线交抛物线与P5、P6,
则这两点的纵坐标是2,
把y=2代入y=-
x2+x+3得:y=-
x2+x+3=2,
解得:x=2±2
,
即P5(2-2
,2),P6(2+2
,2),
∴Q5的坐标是(2
-2,0),Q6的坐标是(-2-2
,0).
综上所述:Q1(2
-2,0),Q2(-2
-2,0),Q3(6-2
,0),Q4(6+2
,0).
|
解得
|
∴抛物线的解析式为y=-
| 1 |
| 4 |
顶点坐标是(2,4);
(2)D(4,3),
设直线AD的解析式为y=kx+b(k≠0),

∵直线经过点A(-2,0)、点D(4,3),
∴
|
∴
|
∴y=
| 1 |
| 2 |
(3)存在.
①如图1,P与M的纵坐标相等,可将M的纵坐标代入抛物线中求出P的坐标,然后可根据M,P的横坐标求出MP的长,即AQ的长,然后根据A的坐标即可求出Q的坐标:Q1(2
| 2 |
②如图2,方法同①,Q2(-2
| 2 |
③如图3,根据平行四边形的对称性,那么M,P的纵坐标互为相反数,因此可求出P的坐标,可先在三角形AOM中求出AO的长,然后A到抛物线对称轴的长+P的横坐标=Q的横坐标,据此可求出Q点的坐标:Q3(6-2
| 6 |
④如图4,可参照③的方法求出P的坐标,然后求出PA的长,即MQ的长,然后可过D作x轴的垂线,通过构建直角三角形求出OQ的长.进而得出Q的坐标:Q4(6+2
| 6 |
⑤以AM为对角线时,把x=2代入y=
| 1 |
| 2 |

即M的坐标是(2,2),
过M作x轴的平行线交抛物线与P5、P6,
则这两点的纵坐标是2,
把y=2代入y=-
| 1 |
| 4 |
| 1 |
| 4 |
解得:x=2±2
| 2 |
即P5(2-2
| 2 |
| 2 |
∴Q5的坐标是(2
| 2 |
| 2 |
综上所述:Q1(2
| 2 |
| 2 |
| 6 |
| 6 |
点评:本题主要考查了二次函数的相关知识,(1)(2)比较简单,要注意的是(3)中要把所有的情况都考虑到不要漏解.

练习册系列答案
相关题目