题目内容
【题目】 已知,如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点, 且∠MAN=45.

(1)求证:MN=BM+DN.
(2)若AM、AN交对角线BD于E、F两点,设BF=y,DE=x,求y与x的函数关系式.
【答案】(1)见解析;(2)![]() ;
;
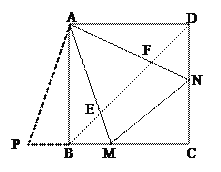
【解析】试题分析:(1)将△ABM绕点A逆时针旋转90°至△ADM′,根据正方形的性质和且∠MAN=45°可进行证明.
(2)证明△BFA∽△DAE,根据相似三角形的对应边成比例,可列出函数式.
试题解析:(1)证明:将△ABM绕点A逆时针旋转90°至△ADM′,如图,
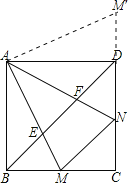
∵∠M′AN=∠DAN+∠MAB=45°,AM′=AM,BM=DM′,
∵M′AN=∠MAN=45°,AN=AN,
∴△AMN≌△AM′N′,
∴MN=NM′,
∴M′N=M′D+DN=BM+DN,
∴MN=BM+DN.
(2)解:∵∠AED=45°+∠BAE,∠FAB=45°+∠BAE,
∴∠AED=∠FAB,
∵∠ABF=∠ADE,
∴△BFA∽△DAE,
∴![]() ,
,
∴![]() ,
,
∴y=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目