题目内容
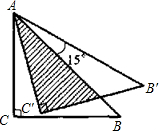 如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=1,则图中阴影部分的面积为( )
如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=1,则图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、3
|
分析:根据旋转的性质可得AC′=AC,∠BAC′=30°,然后利用∠BAC′的正切求出C′D的长度,再利用三角形的面积公式列式计算即可求解.
解答: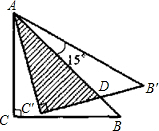 解:根据题意,AC′=AC=1,
解:根据题意,AC′=AC=1,
∵∠B′AB=15°,
∴∠BAC′=45°-15°=30°,
∴C′D=AC′tan30°=
,
∴S阴影=
AC′•C′D=
×1×
=
.
故选B.
 解:根据题意,AC′=AC=1,
解:根据题意,AC′=AC=1,∵∠B′AB=15°,
∴∠BAC′=45°-15°=30°,
∴C′D=AC′tan30°=
| ||
| 3 |
∴S阴影=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 6 |
故选B.
点评:本题考查了旋转的性质,等腰直角三角形的两直角边相等,锐角等于45°的性质,是基础题,难度不大.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
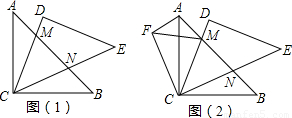
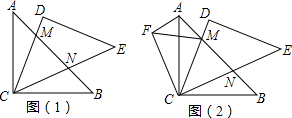 将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.
将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由. 将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.
将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.