题目内容
已知:抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C 在y轴的正半轴上;线段OB,OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
在y轴的正半轴上;线段OB,OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.(1)求此抛物线的表达式;
(2)若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE.当△CEF的面积最大时,求点E的坐标,并求此时面积的最大值;
(3)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点Q,点D的坐标为(-3,0).问:是否存在这样的直线l,使得△ODQ是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
分析:(1)已知了抛物线的对称轴可以用顶点式二次函数通式y=a(x-h)2+b来设抛物线的解析式.然后根据方程x2-10x+16=0,求出B、C两点的坐标,进而可根据B、C的坐标求出抛物线的解析式.
(2)本题可通过设E点的坐标,然后列出关于△CEF的面积和E点横坐标的二次函数式,然后根据函数的性质来确定面积的最大值以及对应的E点的坐标.
(3)本题的关键是求出Q点的纵坐标,可分三种情况进行讨论.
①当DO=DQ时,根据A、D、O的坐标可知AD=OD,那么此时AD=OD=DQ,三角形AQO为直角三角形且与△AOC相似.可根据相似比求出面积比,进而求出三角形AOQ的面积.过Q作AO边上的高QM,即可根据三角形AOQ的面积求出QM的长即Q点的纵坐标.然后代入抛物线的解析式中即可求出P点的坐标.
②当DQ=OQ时,可根据三角形AQM与三角形ACO相似求出QM的长即Q点的纵坐标,然后按①的方法即可得出P点的坐标.
③当OQ=OD时,OQ=OD=3,显然这种情况是不成立的(O到AC的距离为4.8).
综合三种情况即可求出符合条件的P点的坐标.
(2)本题可通过设E点的坐标,然后列出关于△CEF的面积和E点横坐标的二次函数式,然后根据函数的性质来确定面积的最大值以及对应的E点的坐标.
(3)本题的关键是求出Q点的纵坐标,可分三种情况进行讨论.
①当DO=DQ时,根据A、D、O的坐标可知AD=OD,那么此时AD=OD=DQ,三角形AQO为直角三角形且与△AOC相似.可根据相似比求出面积比,进而求出三角形AOQ的面积.过Q作AO边上的高QM,即可根据三角形AOQ的面积求出QM的长即Q点的纵坐标.然后代入抛物线的解析式中即可求出P点的坐标.
②当DQ=OQ时,可根据三角形AQM与三角形ACO相似求出QM的长即Q点的纵坐标,然后按①的方法即可得出P点的坐标.
③当OQ=OD时,OQ=OD=3,显然这种情况是不成立的(O到AC的距离为4.8).
综合三种情况即可求出符合条件的P点的坐标.
解答:解:(1)解方程x2-10x+16=0得x1=2,x2=8.
∵点B在x轴的正半轴上,点C在y轴的正半轴上,且OB<OC,
∴点B的坐标为(2,0),点C的坐标为(0,8).
又∵抛物线y=ax2+bx+c的对称轴是直线x=-2,
∴可设抛物线的表达式为y=a(x+2)2+k.
∵点B(2,0),C(0,8)在抛物线上,
解得a=-
,k=
,
∴所求抛物线的表达式为y=-
(x+2)2+
=-
x2-
x+8.
(2)设点E的坐标为(m,0),过点F作FG⊥x轴(AB),垂足为点G.
由(1)可得,点A的坐标为(-6,0).
∴AB=8,EB=2-m.
∵EF∥AC,
∴△BEF∽△BAC.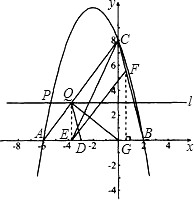
∴
=
,
即
=
,
∴FG=2-m,
∴S=S△BCE-S△BFE=
(2-m)×8-
(2-m)×(2-m)=-
(m2+4m-12)=-
(m+2)2+8.
自变量m的取值范围是-6<m<2,
∴当m=-2时,S有最大值,S最大值=8.
∴点E的坐标为(-2,0).
(3)存在.在△ODQ中,
(Ⅰ)若DO=DQ,
∵A(-6,0),D(-3,0),
∴AD=OD=DQ=3.
∴△AQO是直角三角形.
∴Rt△AOQ∽Rt△ACO,
∴
=(
)2,
由(1)可知AC=10,S△ACO=24,
又∵AO=6,
∴S△AOQ=
,
作QM⊥x轴(OA),垂足为点M.
则S△AOQ=
×6×QM=
,
∴QM=
,
即点Q的纵坐标为
,
由-
(x+2)2+
=
,
解得x1=-2-
,x2=-2+
,
此时,点P的坐标为:P1(-2-
,
)或P2(-2+
,
).
(Ⅱ)若QO=QD,
则QM是等腰△OQD底边上的中线.
∴OM=
OD=
,
∴AM=
,
由于Rt△AMQ∽Rt△AOC,
∴
=
,
即
=
,解得QM=6即点Q的纵坐标为6.
由-
(x+2)2+8=6,
解得x3=-2-
,x4=-2+
,
此时点P的坐标为:P3(-2-
,6)或P4(-2+
,6).
(Ⅲ)若OD=OQ,则OQ=3,
∵点O到AC的距离是
=4.8,而OQ=3<4.8,此时不存在这样的直线l,使△ODQ是等腰三角形.
综上所述,存在这样的直线l,使得△ODQ是等腰三角形.点P的坐标为:P1(-2-
,
)或P2(-2+
,
)或P3(-2-
,6)或P4(-2+
,6).
∵点B在x轴的正半轴上,点C在y轴的正半轴上,且OB<OC,
∴点B的坐标为(2,0),点C的坐标为(0,8).
又∵抛物线y=ax2+bx+c的对称轴是直线x=-2,
∴可设抛物线的表达式为y=a(x+2)2+k.
∵点B(2,0),C(0,8)在抛物线上,
解得a=-
| 2 |
| 3 |
| 32 |
| 3 |
∴所求抛物线的表达式为y=-
| 2 |
| 3 |
| 32 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
(2)设点E的坐标为(m,0),过点F作FG⊥x轴(AB),垂足为点G.
由(1)可得,点A的坐标为(-6,0).
∴AB=8,EB=2-m.
∵EF∥AC,
∴△BEF∽△BAC.

∴
| BE |
| BA |
| FG |
| CO |
即
| 2-m |
| 8 |
| FG |
| 8 |
∴FG=2-m,
∴S=S△BCE-S△BFE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
自变量m的取值范围是-6<m<2,
∴当m=-2时,S有最大值,S最大值=8.
∴点E的坐标为(-2,0).
(3)存在.在△ODQ中,
(Ⅰ)若DO=DQ,
∵A(-6,0),D(-3,0),
∴AD=OD=DQ=3.
∴△AQO是直角三角形.
∴Rt△AOQ∽Rt△ACO,
∴
| S△AOQ |
| S△SCO |
| AO |
| AC |
由(1)可知AC=10,S△ACO=24,
又∵AO=6,
∴S△AOQ=
| 216 |
| 25 |
作QM⊥x轴(OA),垂足为点M.
则S△AOQ=
| 1 |
| 2 |
| 216 |
| 25 |
∴QM=
| 72 |
| 25 |
即点Q的纵坐标为
| 72 |
| 25 |
由-
| 2 |
| 3 |
| 32 |
| 3 |
| 72 |
| 25 |
解得x1=-2-
8
| ||
| 5 |
8
| ||
| 5 |
此时,点P的坐标为:P1(-2-
8
| ||
| 5 |
| 72 |
| 25 |
8
| ||
| 5 |
| 72 |
| 25 |
(Ⅱ)若QO=QD,
则QM是等腰△OQD底边上的中线.
∴OM=
| 1 |
| 2 |
| 3 |
| 2 |
∴AM=
| 9 |
| 2 |
由于Rt△AMQ∽Rt△AOC,
∴
| AM |
| AO |
| QM |
| CO |
即
| ||
| 6 |
| QM |
| 8 |
由-
| 2 |
| 3 |
解得x3=-2-
| 3 |
| 3 |
此时点P的坐标为:P3(-2-
| 3 |
| 3 |
(Ⅲ)若OD=OQ,则OQ=3,
∵点O到AC的距离是
| 6×8 |
| 10 |
综上所述,存在这样的直线l,使得△ODQ是等腰三角形.点P的坐标为:P1(-2-
8
| ||
| 5 |
| 72 |
| 25 |
8
| ||
| 5 |
| 72 |
| 25 |
| 3 |
| 3 |
点评:本题着重考查了待定系数法求二次函数解析式、三角形相似、探究等腰三角形的构成情况等重要知识点,综合性强,能力要求较高.考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
相关题目
 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
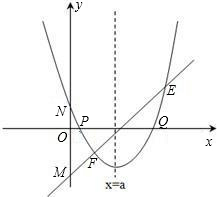
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. (2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.
(2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.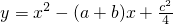 ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边. ,抛物线与x轴交于点P、Q,问是否
,抛物线与x轴交于点P、Q,问是否 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边.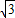 ,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.