题目内容
已知:如图,一块三角板的直角顶点P放在正方形ABCD的AB边上,并且使一条直角边经过点C,三角板 的另一条直角边与AD交于点Q.
的另一条直角边与AD交于点Q.
(1)请你写出此时图形中成立的一个结论(任选一个).
(2)当点P满足什么条件时,有AQ+BC=CQ?请证明你的结论.
(3)当点Q在AD的什么位置时,可证得PC=3PQ?并写出论证的过程.
 解:(1)△APQ∽△BCP.(答案不唯一)
解:(1)△APQ∽△BCP.(答案不唯一)(2)当P为AB中点时,有AQ+BC=CQ.
证明:连接CQ,延长QP,交CB的延长线于点E.
可证△APQ≌△BPE.
则AQ=BE,PQ=PE.
又因为CP⊥QE,可得CQ=CE,
所以AQ+BC=CQ.
(3)当
 时,有PC=3PQ.
时,有PC=3PQ.证明:在正方形ABCD中,∠A=∠B=90°,AD=BC=AB.
又因为直角三角板的顶点P在边AB上,
所以∠1+∠2=180°-∠QPC=90°.
因为Rt△CBP中,∠3+∠2=90°,
所以∠1=∠3.
所以△APQ∽△BCP.
所以
 .因为
.因为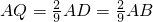 ,
,所以
 .所以
.所以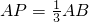 ,或
,或 (不合题意,舍去).
(不合题意,舍去).所以
 .
.所以PC=3PQ.
分析:(1)根据正方形的性质,以及直角三角形的性质即可判断;
(2)连接CQ,延长QP,交CB的延长线于点E.可证△APQ≌△BPE.即可证得:CQ=CE,据此即可证得;
(3)首先证得:△APQ∽△BCP,然后对三角形的对应边,分两种情况讨论即可求解.
点评:本题主要考查了正方形的性质,以及相似三角形的判定与性质,正确进行讨论是关键.

练习册系列答案
相关题目
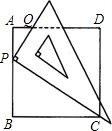 的另一条直角边与AD交于点Q.
的另一条直角边与AD交于点Q.

