Question

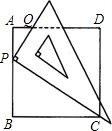
已知：如图，一块三角板的直角顶点P放在正方形ABCD的AB边上，并且使一条直角边经过点C，三角板的另一条直角边与AD交于点Q．

(1)请你写出此时图形中成立的一个结论(任选一个)；

(2)当点P满足什么条件时，有AQ+BC=CQ，请证明你的结论；

(3)当点Q在AD的什么位置时，可证得PC=3PQ，并写出论证的过程．

Answer 1

解：(1)△APQ～△BCP．    

    (2)当P为AB中点时，有AQ+BC=CQ．

证明：连接CQ，延长QP交CB的延长线于点E．

    可证  △APQ≌△BPE．

    则  AQ=BE，PQ=PE，

    又因为  CP⊥QC，可得CQ=CE，

    所以AQ+BC=CQ．            

    (3)当AQ=AD时，有PC=3PQ．    

    证明：在正方形ABCD中，∠A=∠B=90°，AD=BC=AB，

    又因为直角三角板的顶点P在边AB上，

    所以  ∠1+∠2=180°－∠QPC=90°．

    因为  Rt△CBP中，∠3+∠2=90°，

    所以  ∠1=∠3．

    所以  △APQ～△BCP．  

    所以 .

    因为  AQ=，

    所以 .

    所以  AP=AB，或AP= (不合题意，舍去)． 

    所以  .

    所以PC=3PQ．