题目内容
(2002•丽水)已知二次函数y=a(x+m)2+k(a≠0)的图象经过原点,当x=1时,函数y的最小值为-1.(1)求这个二次函数的解析式,并在所给的平面直角坐标系中画出函数图象的草图;
(2)若这个二次函数图象与x轴的交点为A、B,顶点为C,试判断△ABC的形状.
【答案】分析:(1)根据题意可知:抛物线的顶点坐标为(1,-1);因此m=-1,k=-1.然后将原点的坐标代入抛物线的解析式中即可求出抛物线的解析式.
(2)先根据抛物线的解析式求出A、B的坐标,已知了顶点C的坐标,根据三点的坐标进行判断即可.
解答: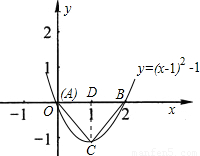 解:(1)由题意可知m=-1,k=-1,将原点坐标代入后可得:
解:(1)由题意可知m=-1,k=-1,将原点坐标代入后可得:
0=a(0-1)2-1,a=1;
因此抛物线的解析式为y=(x-1)2-1.
(2)由(1)的抛物线可知:
当y=0时,0=(x-1)2-1,解得x=0,x=2;
因此A、B的坐标分别为(0,0),(2,0).
已知了C点的坐标为(1,-1).
过C作CD⊥x轴于D,
在直角三角形ADC中,AD=DC,∠ADC=90°,
因此△ADC是等腰直角三角形.
∠CAD=∠ACD=45°;
同理可得∠DBC=∠BCD=45°,
因此△ABC为等腰直角三角形.
点评:本题着重考查了待定系数法求二次函数解析式、等腰直角三角形的判定等知识点,根据已知条件求出抛物线的解析式是解题的关键.
(2)先根据抛物线的解析式求出A、B的坐标,已知了顶点C的坐标,根据三点的坐标进行判断即可.
解答:
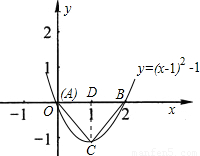 解:(1)由题意可知m=-1,k=-1,将原点坐标代入后可得:
解:(1)由题意可知m=-1,k=-1,将原点坐标代入后可得:0=a(0-1)2-1,a=1;
因此抛物线的解析式为y=(x-1)2-1.
(2)由(1)的抛物线可知:
当y=0时,0=(x-1)2-1,解得x=0,x=2;
因此A、B的坐标分别为(0,0),(2,0).
已知了C点的坐标为(1,-1).
过C作CD⊥x轴于D,
在直角三角形ADC中,AD=DC,∠ADC=90°,
因此△ADC是等腰直角三角形.
∠CAD=∠ACD=45°;
同理可得∠DBC=∠BCD=45°,
因此△ABC为等腰直角三角形.
点评:本题着重考查了待定系数法求二次函数解析式、等腰直角三角形的判定等知识点,根据已知条件求出抛物线的解析式是解题的关键.

练习册系列答案
相关题目
