题目内容
如图,已知抛物线的顶点为M(5,6),且经过点C(-1,0).(1)求抛物线的解析式;
(2)设抛物线与y轴交于点A,过A作AB∥x轴,交抛物线于另一点B,则抛物线上存在点P,使△ABP的面积等于△ABO的面积,请求出所有符合条件的点P的坐标;
(3)将抛物线向右平移,使抛物线经过点(5,0),请直接答出曲线段CM(抛物线图象的一部分,如图中的粗线所示)在平移过程中所扫过的面积.

【答案】分析:(1)设抛物线的解析式为y=a(x-5)2+6,将C(-1,0)代入,利用待定系数法可得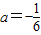 ,则所求抛物线的解析式为
,则所求抛物线的解析式为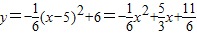 ;
;
(2)先根据函数解析式求得OA=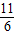 ,结合AB∥x轴,OA⊥AB的性质可知点P到AB的距离为
,结合AB∥x轴,OA⊥AB的性质可知点P到AB的距离为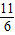 ,设点P的坐标为
,设点P的坐标为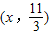 或(x,0),①将
或(x,0),①将 代入
代入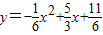 ,解得
,解得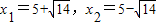
②将(x,0)代入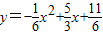 ,解得x3=-1,x4=11,综合可知点P的坐标为
,解得x3=-1,x4=11,综合可知点P的坐标为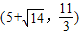 、
、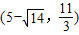 、(-1,0)、(11,0).
、(-1,0)、(11,0).
(3)曲线段CM在平移过程中所扫过的面积可看作为底为6,高为6的平行四边形的面积,故为36.
解答:解:(1)设抛物线的解析式为y=a(x-5)2+6(1分)
将C(-1,0)代入,
得0=a(-1-5)2+6,
解得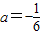 (2分)
(2分)
∴所求抛物线的解析式为 (1分);
(1分);
(2)∵当x=0时,y= ,
,
∴OA=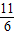 (1分)
(1分)
∵AB∥x轴,
∴OA⊥AB
∵S△ABO=S△ABP
∴点P到AB的距离为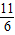 (2分)
(2分)
∴设点P的坐标为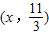 或(x,0)
或(x,0)
将 代入
代入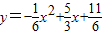 ,
,
解得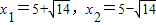 (2分)
(2分)
将(x,0)代入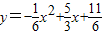 ,
,
解得x3=-1,x4=11(2分)
∴点P的坐标为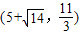 、
、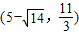 、(-1,0)、(11,0)(1分);
、(-1,0)、(11,0)(1分);
(3)∵曲线段CM在平移过程中所扫过的面积可看作为底为6,高为6的平行四边形的面积,
∴所扫过的面积为36.(2分)
点评:本题考查二次函数的综合应用,其中涉及到的知识点有待定系数法求函数解析式和二次函数和方程之间的关系以及利用数形结合的方法求算几何图形的面积等.要熟练掌握才能灵活运用.
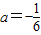 ,则所求抛物线的解析式为
,则所求抛物线的解析式为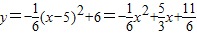 ;
;(2)先根据函数解析式求得OA=
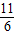 ,结合AB∥x轴,OA⊥AB的性质可知点P到AB的距离为
,结合AB∥x轴,OA⊥AB的性质可知点P到AB的距离为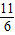 ,设点P的坐标为
,设点P的坐标为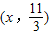 或(x,0),①将
或(x,0),①将 代入
代入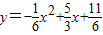 ,解得
,解得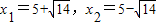
②将(x,0)代入
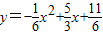 ,解得x3=-1,x4=11,综合可知点P的坐标为
,解得x3=-1,x4=11,综合可知点P的坐标为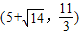 、
、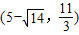 、(-1,0)、(11,0).
、(-1,0)、(11,0).(3)曲线段CM在平移过程中所扫过的面积可看作为底为6,高为6的平行四边形的面积,故为36.
解答:解:(1)设抛物线的解析式为y=a(x-5)2+6(1分)
将C(-1,0)代入,
得0=a(-1-5)2+6,
解得
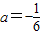 (2分)
(2分)∴所求抛物线的解析式为
 (1分);
(1分);(2)∵当x=0时,y=
 ,
,∴OA=
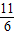 (1分)
(1分)∵AB∥x轴,
∴OA⊥AB
∵S△ABO=S△ABP
∴点P到AB的距离为
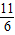 (2分)
(2分)∴设点P的坐标为
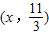 或(x,0)
或(x,0)将
 代入
代入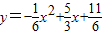 ,
,解得
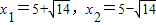 (2分)
(2分)将(x,0)代入
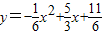 ,
,解得x3=-1,x4=11(2分)
∴点P的坐标为
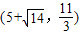 、
、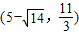 、(-1,0)、(11,0)(1分);
、(-1,0)、(11,0)(1分);(3)∵曲线段CM在平移过程中所扫过的面积可看作为底为6,高为6的平行四边形的面积,
∴所扫过的面积为36.(2分)
点评:本题考查二次函数的综合应用,其中涉及到的知识点有待定系数法求函数解析式和二次函数和方程之间的关系以及利用数形结合的方法求算几何图形的面积等.要熟练掌握才能灵活运用.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
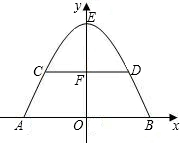
 直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系. 米,旗杆AB高为3米,C点的垂
米,旗杆AB高为3米,C点的垂 直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系. 米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
 米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.