题目内容
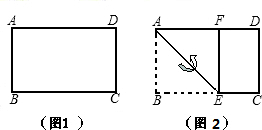
图1是一张宽与长之比为
| ||
| 2 |
分析:本题需先根据四边形ABEF是正方形,得出AB、DC、AF的值,从而得出AF与AD的比值,再根据点F是线段AD的黄金分割点,即可求出FD与DC的比值,即可证出矩形CDFE是黄金矩形.
解答:解:矩形EFDC是黄金矩形,
证明:∵四边形ABEF是正方形,
∴AB=DC=AF,
又∵
=
,
∴
=
,
即点F是线段AD的黄金分割点.
∴
=
=
,
∴
=
,
∴矩形CDFE是黄金矩形.
证明:∵四边形ABEF是正方形,
∴AB=DC=AF,
又∵
| AB |
| AD |
| ||
| 2 |
∴
| AF |
| AD |
| ||
| 2 |
即点F是线段AD的黄金分割点.
∴
| FD |
| AF |
| AF |
| AD |
| ||
| 2 |
∴
| FD |
| DC |
| ||
| 2 |
∴矩形CDFE是黄金矩形.
点评:本题主要考查了黄金分割,在解题时要理解黄金分割的概念,找出黄金分割中成比例的对应线段是解决本题的关键

练习册系列答案
相关题目



 如图,把一张标准纸一次又一次对开,得到“2开”纸,“4开”纸,“8开”纸,“16开”纸….已知标准纸的短边长为a.
如图,把一张标准纸一次又一次对开,得到“2开”纸,“4开”纸,“8开”纸,“16开”纸….已知标准纸的短边长为a.
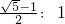 的矩形纸片,我们称这样的矩形为黄金矩形.同学们都知道按图2所示的折叠方法进行折叠,折叠后再展开,可以得到一个正方形ABEF和一个矩形EFDC,那么EFDC这个矩形还是黄金矩形吗?若是,请根据图2证明你的结论;若不是,请说明理由.
的矩形纸片,我们称这样的矩形为黄金矩形.同学们都知道按图2所示的折叠方法进行折叠,折叠后再展开,可以得到一个正方形ABEF和一个矩形EFDC,那么EFDC这个矩形还是黄金矩形吗?若是,请根据图2证明你的结论;若不是,请说明理由.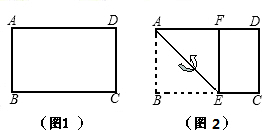
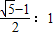 的矩形纸片,我们称这样的矩形为黄金矩形.同学们都知道按图2所示的折叠方法进行折叠,折叠后再展开,可以得到一个正方形ABEF和一个矩形EFDC,那么EFDC这个矩形还是黄金矩形吗?若是,请根据图2证明你的结论;若不是,请说明理由.
的矩形纸片,我们称这样的矩形为黄金矩形.同学们都知道按图2所示的折叠方法进行折叠,折叠后再展开,可以得到一个正方形ABEF和一个矩形EFDC,那么EFDC这个矩形还是黄金矩形吗?若是,请根据图2证明你的结论;若不是,请说明理由.