��Ŀ����
����Ŀ��Ϊ���¹���Ʒ�֣�ij���ƻ��¹���A��B����Ʒ�ֵĹ�������ֲ���������ƻ����������ֹ����繲45�ã�����A����ĵ���Ϊ7Ԫ/�ã�����B�����������y��Ԫ���빺������x���ã�֮�������ͼ��ʾ�ĺ�����ϵ��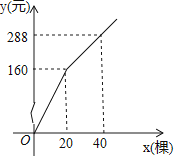
��1����y��x�ĺ�����ϵʽ��
��2�����ڹ���ƻ��У�B���������������35�ã���������A���������������ƹ�����ʹ�ܷ�����ͣ��������ͷ��ã�
���𰸡�
��1��
�⣺��y��x�ĺ�����ϵʽΪ��y=kx+b��
�ѣ�20��160������40��288������y=kx+b�ã�
![]()
��ã� ![]()
��y=6.4x+32
��2��
�⣺��B���������������35�ã���������A�����������
�� ![]()
��22.5��x��35��
���ܷ���ΪWԪ����W=6.4x+32+7��45��x��=��0.6x+347��
��k=��0.6��
��y��x�����������
�൱x=35ʱ��W�ܷ�����ͣ�W���=��0.6��35+347=137��Ԫ��
����������1�����õõ�ϵ���������ʽ���г��������ɣ���2�������������ΪW=A������ķ���+B������ķ��ã����ɽ�𣮴�����Ҫ������һ�κ�����Ӧ�ã�����һ�κ����������Եó�������ʡ�����ǽ������Ĺؼ���

����Ŀ��ijУ�ڼ��С����������ļ�ֵ�ۡ��ݽ������У�������ǰ20����ѡ�ֵ��ۺϷ���m���з���ͳ�ƣ���������ʾ��
��� | ���� | Ƶ�� |
һ | 6��m��7 | 2 |
�� | 7��m��8 | 7 |
�� | 8��m��9 | a |
�� | 9��m��10 | 2 |

��1����a��ֵ��
��2����������ͼ���������������8��m��9������Ӧ������ͼ��Բ�ĽǴ�С��
��3�����ڵ�һ���ڵ�����ѡ�ּ�Ϊ��A1��A2 �� �ڵ������ڵ�����ѡ�ּ�Ϊ��B1��B2 �� �ӵ�һ��͵����������ѡȡ2��ѡ�ֽ��е�����̸�����һ��������1��ѡ�ֱ�ѡ�еĸ��ʣ�����״ͼ���б����г����п��ܽ������