题目内容
【题目】把一条12个单位长度的线段分成三条线段,其中一条线段成为4个单位长度,另两条线段长都是单位长度的整数倍.
(1)不同分段得到的三条线段能组成多少个不全等的三角形?用直尺和圆规作这些三角形(用给定的单位长度,不写作法,保留作图痕迹);
(2)求出(1)中所作三角形外接圆的周长.
【答案】(1)2;(2)作图见解析.
【解析】试题分析:(1)用列举法得出所有不同分法的分法,根据三角形三边关系得出能组成不全等的三角形的个数,应用尺规作图.
(2)由勾股定理逆定理知,3,4,5构成三角形是直角三角形,根据直角三角形斜边上中线等于斜边 一半的性质,知3,4,5构成三角形的外接圆直径等于5,从而根据周长公式求解;对4,4,4构成三角形是等边三角形,根据锐角三角函数定义和特殊角的三角函数值求解即可.
试题解析:(1)∵把一条12个单位长度的线段分成三条线段,其中一条线段长为4个单位长度,另两条线段长都是单位长度的整数倍,
∴不同分法的分法有:1,4,7;2,4,6;3,4,5;4,4,4.
∴能组成2个不全等的三角形:3,4,5;4,4,4.
作图如下:
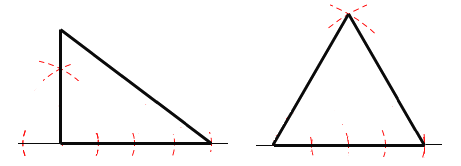
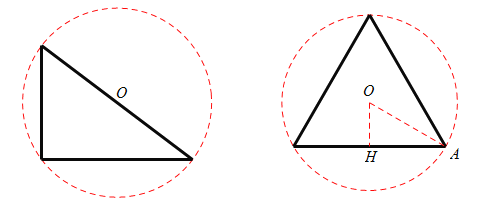
(2)对于3,4,5构成的三角形,由勾股定理逆定理知,它是直角三角形,所以它的外接圆直径等于5.
∴它的三角形外接圆的周长为![]() .
.
对于4,4,4构成的三角形,如图,知AH=2,∠OAH=30°,所以它的外接圆半径等于![]() .
.
∴它的三角形外接圆的周长为![]() .
.

练习册系列答案
相关题目