Question

（2006•遵义）如图．在平面直角坐标系中，矩形ABCO的顶点A、C、O的坐标分别为：A（4，0），C（0，2），O（0，0）．
（1）填空：把矩形ABCO分成面积相等的两部分的直线有______条；这些直线都经过矩形ABCO的______．
（2）若直线y=kx+4（k≠0）把矩形ABCO分成面积相等的两部分，请你在图中画出这条直线，并求出该直线的解析式．

Answer 1

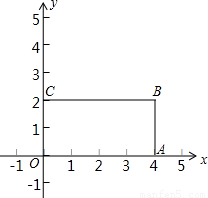
【答案】分析：（1）矩形是中心对称图形，其对称中心是两条对角线的交点，因此，经过对称中心的任意一条直线可以把矩形ABCO分成面积相等的两部分；
（2）根据矩形又是轴对称图形，可确定点P的坐标，从而可确定直线解析式．
解答：解：（1）无数条．
对角线的交点（或对称中心或两组对边中垂线的交点）．

（2）如图，画出直线y=kx+4．
根据三角形中位线性质可知，点P的坐标为（2，1），代入直线y=kx+4中得k=-．
∴所求直线的解析式y=-x+4．
点评：矩形是中心对称图形，一般用待定系数法求解函数解析式．