Question

【题目】将2×2的正方形网格如图放置在平面直角坐标系中，每个小正方形的顶点称为格点，每个小正方形的边长都是1，正方形ABCD的顶点都在格点上．若直线y=kx（k≠0）与正方形ABCD有公共点，则k的取值范围是（ ）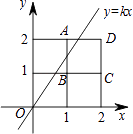

A.k≤2
B.
C.
D.

Answer 1

【答案】C
【解析】解：由题意得：点A的坐标为（1，2），点C的坐标为（2，1），

∵当正比例函数经过点A时，k=2，当经过点C时，k= ，

∴直线y=kx（k≠0）与正方形ABCD有公共点，k的取值范围是 ，

故选C．

【考点精析】认真审题，首先需要了解正比例函数的图象和性质(正比函数图直线，经过一定过原点．K正一三负二四，变化趋势记心间．K正左低右边高，同大同小向爬山．K负左高右边低，一大另小下山峦)．