题目内容
（2011•虹口区二模）如图，⊙O1与⊙02外切于C，AB为⊙O1与⊙O2的外公切线，且A、B为切点．已知CA=4，CB=3，则线段AB的长是 ．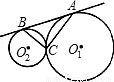
【答案】分析：首先作出两圆的公切线，得出△ABC是直角三角形，再利用勾股定理求出AB的长．
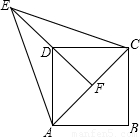
解答：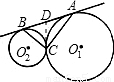
解：过C作两圆的公切线DC，
∵⊙O1与⊙02外切于C，AB为⊙O1与⊙O2的外公切线，CD是两圆的公切线，
∴AC=CD，BD=CD，
∴△ABC是直角三角形，
BC2+AC2=AB2，
∵CA=4，CB=3，
∴AB2=16+9=25，
AB=5．
故答案为：5．
点评：此题主要考查了相切两圆的性质，作出两圆公切线是解决问题的关键，这也是两圆相切时常用辅助线，同学们应学会应用．
解答：
解：过C作两圆的公切线DC，∵⊙O1与⊙02外切于C，AB为⊙O1与⊙O2的外公切线，CD是两圆的公切线，
∴AC=CD，BD=CD，
∴△ABC是直角三角形，
BC2+AC2=AB2，
∵CA=4，CB=3，
∴AB2=16+9=25，
AB=5．
故答案为：5．
点评：此题主要考查了相切两圆的性质，作出两圆公切线是解决问题的关键，这也是两圆相切时常用辅助线，同学们应学会应用．
练习册系列答案
相关题目
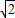，0），点C、D分别在第一、三象限，且此一次函数与反比例函数图象交于C、D两点，又OA=OB=AC=BD．
