题目内容
（2011•虹口区二模）如图，正方形ABCD中，以对角线AC为一边作等边△ACE，连接ED并延长交AC于点F．求证：点F是线段AC中点．
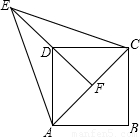
【答案】分析：由正方形ABCD得到AD=CD，等边三角形ACE得到EA=EC，证出△AED和△CED全等，推出∠AEF=∠CEF，即可得出答案．
解答：证明：∵四边形ABCD是正方形
∴AD=CD
又△AEC是等边三角形
∴EA=EC．
又ED是公共边．
∴△AED≌△CED．
∴∠AED=∠CED
又EA=EC
∴EF是△EAC中AC边的中线．
∴点F是线段AC中点．
点评：本题主要考查了正方形的性质，等边三角形的性质，全等三角形的性质和判定，等腰三角形的性质等知识点，解此题的关键是证出∠AED和∠CED相等．题型较好，综合性强．
解答：证明：∵四边形ABCD是正方形
∴AD=CD
又△AEC是等边三角形
∴EA=EC．
又ED是公共边．
∴△AED≌△CED．
∴∠AED=∠CED
又EA=EC
∴EF是△EAC中AC边的中线．
∴点F是线段AC中点．
点评：本题主要考查了正方形的性质，等边三角形的性质，全等三角形的性质和判定，等腰三角形的性质等知识点，解此题的关键是证出∠AED和∠CED相等．题型较好，综合性强．
练习册系列答案
相关题目
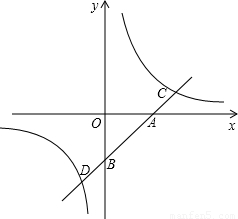
，0），点C、D分别在第一、三象限，且此一次函数与反比例函数图象交于C、D两点，又OA=OB=AC=BD．
