题目内容
【题目】已知∠AOB=150°,OC为∠AOB内部的一条射线,∠BOC=60°.
(1)如图1,若OE平分∠AOB,OD为∠BOC内部的一条射线,∠COD=![]() ∠BOD,求∠DOE的度数;
∠BOD,求∠DOE的度数;
(2)如图2,若射线OE绕着O点从OA开始以15度/秒的速度顺时针旋转至OB结束、OF绕着O点从OB开始以5度秒的速度逆时针旋转至OA结束,运动时间为t秒,当∠EOC=∠FOC时,求t的值:
(3)若射线OM绕着O点从OA开始以15度秒的速度逆时针旋转至OB结束,在旋转过程中,ON平分∠AOM,试问2∠BON一∠BOM在某时间段内是否为定值,若不是,请说明理由;若是请补全图形,求出这个定值并写出t所在的时间段.(本题中的角均为大于0°且小于180°的角)

【答案】(1)35°.(2)当∠EOC=∠FOC时,t=3s或7.5s.(3)①当0<t≤2时,2∠BON﹣∠BOM=150°.当4<t<12时,2∠BON﹣∠BOM=210°.
【解析】
(1)根据∠EOD=∠EOB﹣∠DOB,只要求出∠EOB,∠DOB即可;
(2)分两种情形列出方程即可解决问题;
(3)①当0<t≤2时,2∠BON﹣∠BOM=150°.②当4<t<12时,2∠BON﹣∠BOM=210°.用t表示∠BON、∠BOM,求2∠BON一∠BOM的值即可;
解:(1)∵∠AOB=150°,OE平分∠AOB,
∴∠EOB=![]() ∠AOB=75°,
∠AOB=75°,
∵∠BOC=60°,∠COD=![]() ∠BOD,
∠BOD,
∴∠BOD=40°,∠COD=20°,
∴∠EOD=∠EOB﹣∠DOB=75°﹣40°=35°.
(2)当OE在∠AOC内部时,∵∠EOC=∠FOC,
∴90﹣15t=60﹣5t,
∴t=3.
当OE与OF重合时,15t+5t=150°,
t=7.5.
综上所述,当∠EOC=∠FOC时,t=3s或7.5s.
(3)①当0<t≤2时,2∠BON﹣∠BOM=150°.
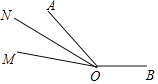
理由:∵∠AOM=15t.∠AON=∠MON=7.5t,∠BON=150°+7.5t,∠BOM=150°+15t,
∴2∠BON一∠BOM=2(150°+7.5t)﹣(150°+15t)=150°
②当4<t<12时,2∠BON﹣∠BOM=210°.
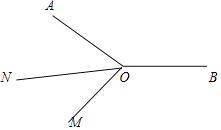
理由:∵∠AOM=15t.∠AON=∠MON=7.5t,∠BON=210°﹣7.5t,∠BOM=210°﹣15t,
∴2∠BON一∠BOM=2(210°﹣7.5t)﹣(210°﹣15t)=210°(4<t<12).

【题目】将一张正方形纸片剪成四个大小、形状一样的小正方形(如图所示),记为第一次操作,然后将其中的一片又按同样的方法剪成四小片,记为第二次操作,如此循环进行下去.请将下表中空缺的数据填写完整,并解答所提出的问题:
操作次数 | 1 | 2 | 3 | 4 | … |
正方形个数 | 4 | 7 |
|
| … |
(1)如果剪100次,共能得到 个正方形;
(2)如果剪n次共能得到bn个正方形,试用含有n、bn的等式表示它们之间的数量关系 ;
(3)若原正方形的边长为1,设an表示第n次所剪的正方形的边长,试用含n的式子表示an ;
(4)试猜想a1+a2+a3+a4+…+an﹣1+an与原正方形边长的数量关系,并用等式写出这个关系 .



