题目内容
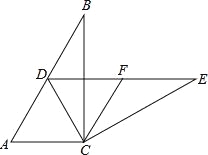
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
【答案】(1)、n=60;(2)、菱形;证明过程见解析
【解析】
试题分析:(1)、利用旋转的性质得出AC=CD,进而得出△ADC是等边三角形,即可得出∠ACD的度数;
(2)、利用直角三角形的性质得出FC=DF,进而得出AD=AC=FC=DF,即可得出答案.
试题解析:(1)、∵在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC, ∴AC=DC,∠A=60°, ∴△ADC是等边三角形, ∴∠ACD=60°, ∴n的值是60;
(2)、四边形ACFD是菱形; 理由:∵∠DCE=∠ACB=90°,F是DE的中点, ∴FC=DF=FE,
∵∠CDF=∠A=60°, ∴△DFC是等边三角形, ∴DF=DC=FC, ∵△ADC是等边三角形,
∴AD=AC=DC, ∴AD=AC=FC=DF, ∴四边形ACFD是菱形.

练习册系列答案
相关题目
【题目】丽华根据演讲比赛中九位评委所给的分数作了如下表格:
平均数 | 中位数 | 众数 | 方差 |
8.5 | 8.3 | 8.1 | 0.15 |
如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
A.平均数
B.众数
C.方差
D.中位数