题目内容
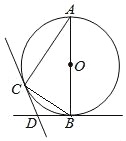
【题目】如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=120°,连接AC.
(1)求∠A的度数;
(2)若点D到BC的距离为2,那么⊙O的半径是多少?
【答案】(1)30°;(2)4![]()
【解析】
试题分析:(1)首先连接OC,由BD,CD分别是过⊙O上点B,C的切线,可求得∠BOC的度数,然后由圆周角定理,求得答案;(2)首先求得∠DCB与∠DBC的度数,然后过点D作DE⊥BC,垂足为E,则DE=2,即可求得BE的长,继而求得BC的长,然后由(1)可知△OBC为等边三角形,即可求得答案.
试题解析:(1)连接OC, ∵BD,CD分别是过⊙O上点B,C的切线, ∴OC⊥CD,OB⊥BD,
∴∠OCD=∠OBD=90°, ∵∠BDC=120°, ∴∠BOC=360°﹣∠OCD﹣∠BDC﹣∠OBD=60°,
∴∠A=![]() ∠BOC=30°;
∠BOC=30°;
(2)∵BD,CD分别是过⊙O上点B,C的切线, ∴DC=DB,
∴∠DCB=∠DBC=![]() (180°﹣120°)=30°, 过点D作DE⊥BC,垂足为E,则DE=2, ∵∠DBC=30°,
(180°﹣120°)=30°, 过点D作DE⊥BC,垂足为E,则DE=2, ∵∠DBC=30°,
∴BD=2DE=4, 在直角△DEB中,BE=2![]() , ∴BC=2BE=4
, ∴BC=2BE=4![]() ,
,
由(1)可知△OBC为等边三角形, ∴OB=BC=4![]() , ∴⊙O的半径是4
, ∴⊙O的半径是4![]() .
.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目