Question

【题目】（问题发现）

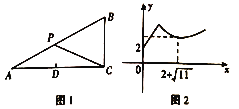
（1）如图1所示，在中，，，点为上一点，作，交于点，则________；

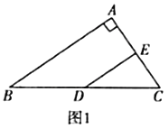
（类比研究）

（2）将绕点顺时针旋转到图2所示位置，此时（1）中的结论还成立吗？请说明理由；

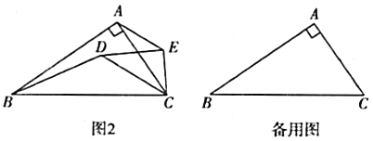
（拓展延伸）

（3）若点为边中点，在绕点旋转的过程中，当、、三点共线时，求的长．

Answer 1

【答案】（1）2；（2）成立；理由见详解；（3）BD的长为或.

【解析】

（1）根据ED∥AB，得出，结合三角函数的定义计算sin30°即可；

（2）根据在Rt△BAC和Rt△DEC中，BC=2AC，DC=2EC，由旋转性质推出△BDC∽△AEC即可得出结论成立；

（3）当B、D、E三点共线时，由旋转性质构图如下，分两种情况讨论：

①旋转至图②中△CED的位置时，在Rt△BEC和Rt△DEC中，分别利用勾股定理计算BE、BD，然后求线段差即可；

②旋转至图②中△C的位置时，由切线长定理知BE=B，然后计算线段和即可．

（1）∵ED∥AB，∠B=30°，AC=2，∠A=90°，

∴，

∴，

故答案为：2；

（2）成立．理由如下：

∵∠ABC=30°，∠EDC=30°，

∴在Rt△BAC和Rt△DEC中，BC=2AC，DC=2EC，

由旋转性质知，∠BCD=∠ACE，

∴△BDC∽△AEC，

∴，

故答案为：成立；

（3）当B、D、E三点共线时，由旋转性质构图如下，分两种情况

①旋转至图②中△CED的位置时，在Rt△ABC中，BC=2AC=4，

∵点E为AC中点，

∴CE=1，

∴在Rt△BEC中，BE=，

∵在Rt△DEC中，EC=1，∠EDC=30°，

∴DE=，

∴BD=；

②旋转至图②中△C的位置时，由切线长定理知BE=B=，

∴由①知，B，

综上所述，BD的长为或，

故答案为：；．