题目内容
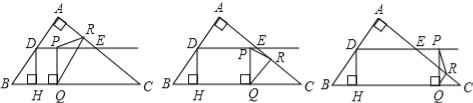
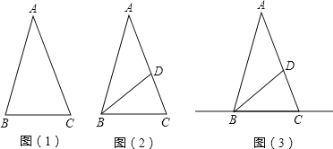
【题目】如图(1),在△ABC中,AB=AC,∠A=36°.
(1)直接写出∠ABC的度数;
(2)如图(2),BD是△ABC中∠ABC的平分线.
①找出图中所有等腰三角形(等腰三角形ABC除外),并选其中一个写出推理过程;
②在直线BC上是否存在点P,使△CDP是以CD为一腰的等腰三角形?如果存在,请在图(3)中画出满足条件的所有的点P,并直接写出相应的∠CPD的度数;如果不存在,请说明理由.
【答案】(1)72°;(2)①△ADB、△BCD是等腰三角形,理由详见解析;②存在3个点P,使得△CDP是等腰三角形,∠CPD的度数详见解析.
【解析】
(1)由已知条件结合等腰三角形的性质及三角形内角和进行求解;
(2)①等腰三角形的判定,BD是△ABC中∠ABC的平分线.可求出各个角的大小再进行判断;
②使△CDP为等腰三角形,则可能是CD=CP,DP=CD,因为∠C=∠BDC,所以不可能PC=PD.
解:(1)∵AB=AC,∠A=36°,∴∠ABC=![]() (180°∠A)==72°;
(180°∠A)==72°;
(2)①如图(2),△ADB、△BCD是等腰三角形.
说明△ADB是等腰三角形,理由:由(1)得:∠ABC=72°,
又∵BD是∠ABC的平分线,∴∠ABD=![]() ∠ABC=36°,
∠ABC=36°,
又∵∠A=36°,∴∠A=∠ABD,
∴AD=BD,即△ADB是等腰三角形;
说明△BCD是等腰三角形,理由:
∵∠A=36°,AB=AC,
∴∠C=∠ABC=![]() (180°-36°)=72°
(180°-36°)=72°
又∵BD是∠ABC的平分线,
∴∠DBC=![]() ∠ABC=36°,
∠ABC=36°,
∴∠BDC=180°-∠C-∠DBC=180°-72°-36°=72°,
∴∠C=∠BDC,
∴BD=BC,即△BCD是等腰三角形;
②存在3个点P,使得△CDP是等腰三角形.如图:
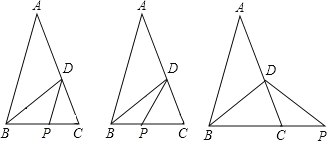
当以∠CDP为顶角,CD为一腰时,∠CPD=72°;
当以∠DCP为顶角,CD为一腰时,存在两点P:
一点在线段BC延长线上,此时∠CPD=36°;
一点在线段BC上,此时∠CPD=54°.
故答案为:(1)72°;(2)①△ADB、△BCD是等腰三角形,理由详见解析;②存在3个点P,使得△CDP是等腰三角形,∠CPD的度数详见解析.

 阅读快车系列答案
阅读快车系列答案