题目内容
(2008•达州)如图,将△AOB置于平面直角坐标系中,其中点O为坐标原点,点A的坐标为(3,0),∠ABO=60度.(1)若△AOB的外接圆与y轴交于点D,求D点坐标.
(2)若点C的坐标为(-1,0),试猜想过D,C的直线与△AOB的外接圆的位置关系,并加以说明.
(3)二次函数的图象经过点O和A且顶点在圆上,求此函数的解析式.

【答案】分析:(1)∠ABO=60°则∠ADO=60°,在直角△AOD中,根据三角函数就可以求出OD的长,则可以求出D的坐标.
(2)若点C的坐标为(-1,0),在直角△CDO中,根据三角函数就可以求出∠CDO的度数.进而得到∠CDA的度数.从而判断过D,C的直线与△AOB的外接圆的位置关系.
(3)函数经过O,A两点,因而对称轴是OA的垂直平分线与圆的交点,过交点作OA的垂线,利用三角函数,就可以求出OA的垂直平分线与圆的交点的坐标,再根据待定系数法就可以求出函数的解析式.
解答: 解:(1)连接AD,则∠ADO=∠B=60°,
解:(1)连接AD,则∠ADO=∠B=60°,
在Rt△ADO中,∠ADO=60°,
所以OD=OA÷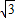 =3÷
=3÷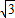 =
=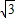 ,
,
所以D点的坐标是(0,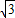 );
);
(2)猜想:CD与圆相切,
∵∠AOD是直角,
∴AD是圆的直径,
又∵tan∠CDO=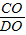 =
=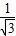 =
=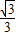 ,∠CDO=30°,
,∠CDO=30°,
∴∠CDA=∠CDO+∠ADO=90°,即CD⊥AD,
∴CD切外接圆于点D;
(3)依题意可设二次函数的解析式为:
y=α(x-0)(x-3),
由此得顶点坐标的横坐标为:x=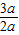 =
= ;
;
即顶点在OA的垂直平分线上,作OA的垂直平分线EF,
则得∠EFA= ∠B=30°,
∠B=30°,
即得到EF=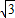 EA=
EA=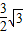 可得一个顶点坐标为(
可得一个顶点坐标为( ,
,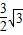 ),
),
同理可得另一个顶点坐标为( ,
,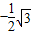 ),
),
分别将两顶点代入y=α(x-0)(x-3)
可解得α的值分别为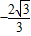 ,
, ,
,
则得到二次函数的解析式是y=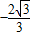 x(x-3)或y=
x(x-3)或y=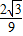 x(x-3).
x(x-3).
点评:本题是二次函数与圆相结合的题目,主要考查了切线的判定方法,待定系数法求函数的解析式.
(2)若点C的坐标为(-1,0),在直角△CDO中,根据三角函数就可以求出∠CDO的度数.进而得到∠CDA的度数.从而判断过D,C的直线与△AOB的外接圆的位置关系.
(3)函数经过O,A两点,因而对称轴是OA的垂直平分线与圆的交点,过交点作OA的垂线,利用三角函数,就可以求出OA的垂直平分线与圆的交点的坐标,再根据待定系数法就可以求出函数的解析式.
解答:
 解:(1)连接AD,则∠ADO=∠B=60°,
解:(1)连接AD,则∠ADO=∠B=60°,在Rt△ADO中,∠ADO=60°,
所以OD=OA÷
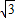 =3÷
=3÷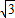 =
=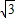 ,
,所以D点的坐标是(0,
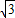 );
);(2)猜想:CD与圆相切,
∵∠AOD是直角,
∴AD是圆的直径,
又∵tan∠CDO=
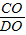 =
=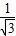 =
=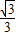 ,∠CDO=30°,
,∠CDO=30°,∴∠CDA=∠CDO+∠ADO=90°,即CD⊥AD,
∴CD切外接圆于点D;
(3)依题意可设二次函数的解析式为:
y=α(x-0)(x-3),
由此得顶点坐标的横坐标为:x=
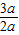 =
= ;
;即顶点在OA的垂直平分线上,作OA的垂直平分线EF,
则得∠EFA=
 ∠B=30°,
∠B=30°,即得到EF=
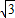 EA=
EA=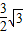 可得一个顶点坐标为(
可得一个顶点坐标为( ,
,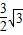 ),
),同理可得另一个顶点坐标为(
 ,
,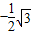 ),
),分别将两顶点代入y=α(x-0)(x-3)
可解得α的值分别为
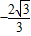 ,
, ,
,则得到二次函数的解析式是y=
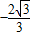 x(x-3)或y=
x(x-3)或y=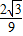 x(x-3).
x(x-3).点评:本题是二次函数与圆相结合的题目,主要考查了切线的判定方法,待定系数法求函数的解析式.

练习册系列答案
相关题目