题目内容
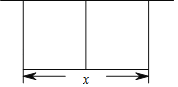
【题目】某农场拟建两间矩形种牛饲养室,饲养室的一面靠现有墙(墙长>50m),中间用一道墙隔开(如图),已知计划中的建筑材料可建围墙的总长为50m,设两饲养室合计长x(m),总占地面积为y(m2)
(1)求y关于x的函数表达式和自变量的取值范围;
(2)若要使两间饲养室占地总面积达到200m2,则各道墙的长度为多少?占地总面积有可能达到210m2吗?
【答案】(1)y=![]() x2+
x2+![]() x,(0<x<50);(2) 各道墙长分别为20米、10米或30米、
x,(0<x<50);(2) 各道墙长分别为20米、10米或30米、![]() 米;占地面积不可能达到210平方米;
米;占地面积不可能达到210平方米;
【解析】
(1)首先根据总长求出长和宽,即可得出函数关系式;
(2)由(1)中的函数解析式代入,然后利用判别式判定,即可得解.
(1)∵围墙的总长为50米,2间饲养室合计长x米,
∴饲养室的宽=![]() 米,
米,
∴总占地面积为y=x![]() =﹣
=﹣![]() x2+
x2+![]() x,(0<x<50);
x,(0<x<50);
(2)当两间饲养室占地总面积达到200平方米时,则﹣![]() x2+
x2+![]() x=200,
x=200,
解得:x=20或30;
答:各道墙长分别为20米、10米或30米、![]() 米;
米;
当占地面积达到210平方米时,则﹣![]() x2+
x2+![]() x=210,
x=210,
方程的△<0,所以此方程无解,
所以占地面积不可能达到210平方米;

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目