Question

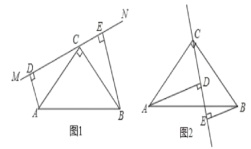
【题目】如图，正方形的边长为，点为上任意一点（可以与点或重合），分别过，，作射线的垂线，垂足分别是，，，则的最大值与最小值的和为________．

Answer 1

【答案】

【解析】

连接AC，DP，根据正方形的性质可得出AB=CD，S正方形ABCD=1，由三角形的面积公式即可得出，结合AP的取值范围即可得出BB′+CC′+DD′的范围，将其最大值与最小值相加即可得出结论．

连接AC,DP,如图所示。

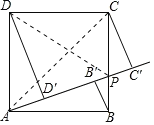
∵四边形ABCD是正方形，正方形ABCD的边长为1，

∴AB=CD,S正方形ABCD=1，

∵S△ADP=S正方形ABCD=,S△ABP+S△ACP=S△ABC=S正方形ABCD=，

∴S△ADP+S△ABP+S△ACP=1，

∴APBB′+APCC′+APDD′=AP(BB′+CC′+DD′)=1，

则 ，

∵

∴当P与B重合时,有最大值2;当P与C重合时,有最小值.

∴

∴BB′+CC′+DD′的最大值与最小值的和为,.

故答案为：