题目内容
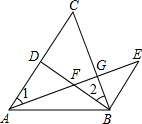 已知:如图,D是AC上一点,BE∥AC,BE=AD,AE分别交BD、BC于点F、G,∠1=∠2.
已知:如图,D是AC上一点,BE∥AC,BE=AD,AE分别交BD、BC于点F、G,∠1=∠2.(1)图中哪个三角形与△FAD全等?证明你的结论;
(2)探索线段BF、FG、EF之间的关系,并说明理由.
分析:(1)已知有一组对顶角和一对边相等,根据平行线的性质又可得到一组角相等,则利用AAS判定△FEB≌△FAD;
(2)根据有两组角对应相等的两个三角形相似,可得到△BFG∽△EFB,根据相似三角形的对应边成比例即可得到BF2=FG•EF.
(2)根据有两组角对应相等的两个三角形相似,可得到△BFG∽△EFB,根据相似三角形的对应边成比例即可得到BF2=FG•EF.
解答:解:(1)△FEB≌△FAD.
证明:∵AD∥BE,
∴∠1=∠E.
又∠EFB=∠AFD,BE=AD,
∴△FEB≌△FAD;
(2)BF2=FG•EF.理由:
∵∠1=∠E,∠1=∠2,
∴∠2=∠E.
又∵∠GFB=∠BFE,
∴△BFG∽△EFB,
∴
=
,
即BF2=FG•EF.
证明:∵AD∥BE,
∴∠1=∠E.
又∠EFB=∠AFD,BE=AD,
∴△FEB≌△FAD;
(2)BF2=FG•EF.理由:
∵∠1=∠E,∠1=∠2,
∴∠2=∠E.
又∵∠GFB=∠BFE,
∴△BFG∽△EFB,
∴
| BF |
| EF |
| FG |
| BF |
即BF2=FG•EF.
点评:此题考查学生对全等三角形的判定及相似三角形的判定的掌握情况.

练习册系列答案
相关题目
 已知:如图,BD是AC边上的高,DE⊥BC于E,BE:EC=5:1.若AD=2,AB=8.
已知:如图,BD是AC边上的高,DE⊥BC于E,BE:EC=5:1.若AD=2,AB=8.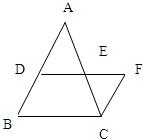 22、已知,如图,E是AC的中点,CF∥AB,求证:CF=AD.
22、已知,如图,E是AC的中点,CF∥AB,求证:CF=AD. 已知:如图,D是AC上一点,BE∥AC,BE=AD,AE分别交BD、BC于点F、G,且∠1=∠2.
已知:如图,D是AC上一点,BE∥AC,BE=AD,AE分别交BD、BC于点F、G,且∠1=∠2.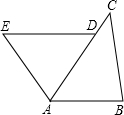 (2013•北京)已知:如图,D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE.
(2013•北京)已知:如图,D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE.