题目内容
 (1)计算:
(1)计算:| 1 |
| 2 |
| 3 |
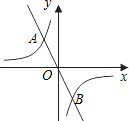
(2)反比例函数的图象与正比例函数的图象相交于A、B两点,若点A在第二象限,且点A的横坐标为-1,且AD⊥x轴,垂足为D,△AOD的面积是2,求点B的坐标.
分析:(1)利用特殊角的三角函数值计算;(2)利用正比例函数与反比例函数图象关于原点对称解答.
解答:解:(1)原式=
×
-
×
=-
;
(2)设反比例函数为y=
(k≠0),正比例函数为y=ax(a≠0);
∵这两个函数的图象关于原点对称,
∴A和B这两点应该是关于原点对称的,B点的横坐标为1,
由图形可知,AD就是A点的纵坐标y,而AD边上的高就是A、B两点横坐标间的距离,即是2,
这样可以得到S=
×2y=2,解得y=2.
∴A点坐标是(-1,2);B点的坐标是(1,-2).
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 11 |
| 4 |
(2)设反比例函数为y=
| k |
| x |
∵这两个函数的图象关于原点对称,
∴A和B这两点应该是关于原点对称的,B点的横坐标为1,
由图形可知,AD就是A点的纵坐标y,而AD边上的高就是A、B两点横坐标间的距离,即是2,
这样可以得到S=
| 1 |
| 2 |
∴A点坐标是(-1,2);B点的坐标是(1,-2).
点评:本题涉及到以下知识点:(1)特殊角的三角函数值;(2)正比例函数与反比例函数的均图象关于原点对称.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
