题目内容
如图所示,若直线a,b分别与直线c,d相交,且∠1+∠3=90°,∠2-∠3=90°,∠4=115°,那么∠3=__________.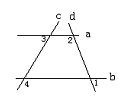

65°
由∠1+∠3=90°,∠2-∠3=90°,可得∠1+∠2=180°,则可得出a∥b,根据同旁内角互补即可得出答案.
解:∵∠1+∠3=90°,∠2-∠3=90°,∴∠1+∠2=180°,
∴∠1的对顶角+∠2=180°,
∴a∥b,∴∠3+∠4的对顶角=180°,
∵∠4=115°,∴∠3=180°-∠4=65°,
故答案为:65°.
本题考查了平行线的判定与性质,属于基础题,关键是正确理解与运用平行线的判定与性质.
解:∵∠1+∠3=90°,∠2-∠3=90°,∴∠1+∠2=180°,
∴∠1的对顶角+∠2=180°,
∴a∥b,∴∠3+∠4的对顶角=180°,
∵∠4=115°,∴∠3=180°-∠4=65°,
故答案为:65°.
本题考查了平行线的判定与性质,属于基础题,关键是正确理解与运用平行线的判定与性质.

练习册系列答案
相关题目
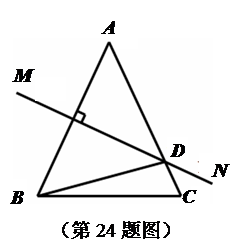
 AB,D为AC的中点,
AB,D为AC的中点,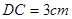 ,则AB的长是( )
,则AB的长是( )

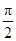 B.
B.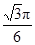
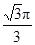 D.
D.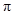
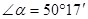 ,则它的余角等于________;
,则它的余角等于________;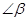 的补角是
的补角是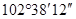 ,则
,则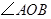 为直角,
为直角,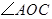 为锐角,且
为锐角,且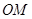 平分
平分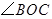 ,
,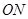 平分
平分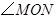 的度数.
的度数.