题目内容
如图,PA、PB与⊙O相切,切点分别为A、B,PA=3,∠P=60°,若AC为⊙O的直径,则图中阴影部分的面积为( )

A.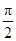 B.
B.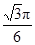
C.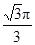 D.
D.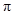

A.
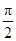 B.
B.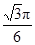
C.
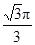 D.
D.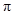
A
∵PA、PB与⊙O相切,
∴PA=PB,∠PAO=∠PBO=90°
∵∠P=60°,
∴△PAB为等边三角形,∠AOB=120°
∴AB=PA=3,∠OBC=60°
∵OB=OC
∴△OBC为等边三角形
∴∠OCB=60°
∵AC为⊙O的直径,
∴∠ABC=90°.
∴OB=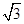
∵OA=OC,
∴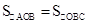
∴S阴影=S扇形OBC=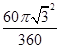 =
=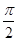 故选A.
故选A.
∴PA=PB,∠PAO=∠PBO=90°
∵∠P=60°,
∴△PAB为等边三角形,∠AOB=120°
∴AB=PA=3,∠OBC=60°
∵OB=OC
∴△OBC为等边三角形
∴∠OCB=60°
∵AC为⊙O的直径,
∴∠ABC=90°.
∴OB=
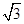
∵OA=OC,
∴
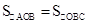
∴S阴影=S扇形OBC=
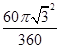 =
=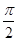 故选A.
故选A.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
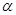 是 ( )
是 ( )
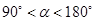
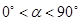
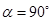

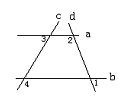
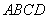 中,
中,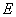 与
与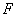 分别是
分别是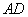 、
、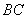 上一点.在
上一点.在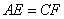 、 ②
、 ② 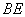 ∥
∥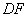 、 ③
、 ③ 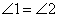 中,
中,