题目内容
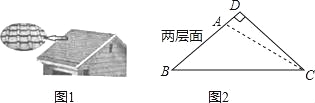
【题目】(2016浙江省舟山市第19题)太阳能光伏建筑是现代绿色环保建筑之一,老张准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°,求改建后南屋面边沿增加部分AD的长.(结果精确到0.1米)
(参考数据:sin18°≈0.31,cos18°≈0.95.tan18°≈0.32,sin36°≈0.59.cos36°≈0.81,tan36°≈0.73)
【答案】1.9米
【解析】
试题分析:在直角三角形BCD中,由BC与sinB的值,利用锐角三角函数定义求出CD的长,在直角三角形ACD中,由∠ACD度数,以及CD的长,利用锐角三角函数定义求出AD的长即可.
试题解析:∵∠BDC=90°,BC=10,sinB=![]() , ∴CD=BCsinB=10×0.59=5.9,
, ∴CD=BCsinB=10×0.59=5.9,
∵在Rt△BCD中,∠BCD=90°﹣∠B=90°﹣36°=54°, ∴∠ACD=∠BCD﹣∠ACB=54°﹣36°=18°,
∴在Rt△ACD中,tan∠ACD=![]() , ∴AD=CDtan∠ACD=5.9×0.32=1.888≈1.9(米),
, ∴AD=CDtan∠ACD=5.9×0.32=1.888≈1.9(米),
则改建后南屋面边沿增加部分AD的长约为1.9米.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目

