题目内容
(1)计算: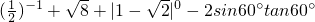 .
.
(2)解方程: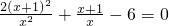 .
.
解:(1)原式=2+2 +1-2×
+1-2× ×
×
=2+2 +1-3
+1-3
=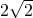 ;
;
(2)设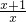 =y,则原方程转化为2y2+y-6=0,
=y,则原方程转化为2y2+y-6=0,
解得,y= 或y=-2,
或y=-2,
当y= 时,
时,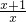 =
= ,解得x=2;
,解得x=2;
当y=-2时,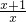 =-2,解得x=-
=-2,解得x=- .
.
经检验,x1=2,x2=- 是原方程的解.
是原方程的解.
故答案为:2 ;x1=2,x2=-
;x1=2,x2=- .
.
分析:(1)分别根据负整数指数幂、二次根式的化简、0指数幂及特殊角的三角函数值计算出各数,再根据实数的运算法则求得计算结果;
(2)先设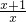 =y,把原式化为关于y的一元二次方程,求出y的值代入y即可求出x的值,最后要把x的值代入原方程进行检验.
=y,把原式化为关于y的一元二次方程,求出y的值代入y即可求出x的值,最后要把x的值代入原方程进行检验.
点评:本题考查的是特殊角的三角函数值及用换元法解分式方程,特别要注意在解(2)时要注意验根.
 +1-2×
+1-2× ×
×
=2+2
 +1-3
+1-3=
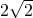 ;
;(2)设
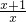 =y,则原方程转化为2y2+y-6=0,
=y,则原方程转化为2y2+y-6=0,解得,y=
 或y=-2,
或y=-2,当y=
 时,
时,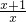 =
= ,解得x=2;
,解得x=2;当y=-2时,
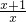 =-2,解得x=-
=-2,解得x=- .
.经检验,x1=2,x2=-
 是原方程的解.
是原方程的解.故答案为:2
 ;x1=2,x2=-
;x1=2,x2=- .
.分析:(1)分别根据负整数指数幂、二次根式的化简、0指数幂及特殊角的三角函数值计算出各数,再根据实数的运算法则求得计算结果;
(2)先设
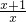 =y,把原式化为关于y的一元二次方程,求出y的值代入y即可求出x的值,最后要把x的值代入原方程进行检验.
=y,把原式化为关于y的一元二次方程,求出y的值代入y即可求出x的值,最后要把x的值代入原方程进行检验.点评:本题考查的是特殊角的三角函数值及用换元法解分式方程,特别要注意在解(2)时要注意验根.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目